Genetic Algorithms#
The genetic algorithm is a probabilistic search algorithm that iteratively transforms a set (called a population) of mathematical objects (typically fixed-length binary character strings), each with an associated fitness value, into a new population of offspring objects using the Darwinian principle of natural selection and using operations that are patterned after naturally occurring genetic operations, such as crossover (sexual recombination) and mutation.)
In this section, we will demonstrate some basic implementations of Simple Genetic Algorithms (SGA), Real-valued GA, as well as the use of GA to generate permutations. At the end, we’ll show how real-valued GA can be applied to a shortest-path search.
Example: Bike pricing using Simple Genetic Algorithm#
Assume that a company wants to design a new bicycle, and needs to consider the following costs:
$700,000 for manufacturing setup, marketing, etc.
$110 for each bike produced
Based on similar bikes, the company expects sales to follow this demand curve:
\(Q= 70,000 - 200P\),
where \(P\) is the price, and \(Q\) is the number of units sold at that price
For example:
At $0, the company would give away 70,000 bikes for free
At $300, the company would sell \(70,000-200*300=10,000\) bikes
At $350, the company wouldn’t sell at anything at all.
Profit would be calculated as following:
\(Profit=Sales-Costs\)
\(Profit=P(70,000-200P)-(700,000+110(70,000-200P))\)
\(Profit=-200P^2+92,000P-8,400,000\)
Simple Genetic Algorithms represent genes as binary values, and mutates those genes through binary operations. Essentially, they replicate the behaviour of genotypes in genetics, where genotypes (actual DNA coding) produce phenotypes (genetic traits).
import random
import math
from tqdm.notebook import tqdm
from copy import copy
import matplotlib.pyplot as plt
Initial Population#
# Generate an initial random population
def init_pop(pop_size, chromosome_length):
ints = [random.randint(0,350) for i in range(pop_size)]
strs = [bin(n)[2:].zfill(chromosome_length) for n in ints]
bins = [[int(x) for x in n] for n in strs]
return bins
Fitness Function#
# For a given population, calculate the fitness of each element in the population
def fitness_score(population):
fitness_values = []
num = []
for i in range(len(population)):
num.append(int("".join(str(x) for x in population[i]), base=2)) # convert binary to decimal
fitness_values.append(-200 * math.pow(num[i],2) + 92000 * num[i] - 8400000)
tuples = zip(*sorted(zip(fitness_values,population),reverse=True))
fitness_values, population = [list(t) for t in tuples]
return fitness_values, population
This fitness function essentially determines how “good” a particular offspring is. It first converts each unit in the population to a binary number (the genotype), and then returns the “best” offspring.
Parent Selection, Crossover, and Mutation#
# Random parent selection
def select_parent(population, num_parents):
parents=random.sample(population, num_parents)
return parents
# Apply 1-point crossover
def crossover(parents, crossover_prob):
chromosome_length = len(parents[0])
if crossover_prob > random.random():
cross_point = random.randint(0,chromosome_length)
parents+= tuple([(parents[0][0:cross_point +1] +parents[1][cross_point+1:(chromosome_length+1)])])
parents+= tuple([(parents[1][0:cross_point +1] +parents[0][cross_point+1:(chromosome_length+1)])])
return parents
The crossover function here first determines if a crossover takes place (using the crossover_prob) and then selects a random crossover point in the chromosome. Using 1-point crossover, the bottom halves are switched the parents.
# Alter each gene independently with a probability mutation_prob
def mutation(population, mutation_prob) :
chromosome_length = len(population[0])
for i in range(len(population)-1) :
for j in range(chromosome_length-1) :
if mutation_prob > random.random():
if population[i][j]==1:
population[i][j]=0
else:
population[i][j]=1
return population
Solution Function#
def SGA(population, num_gen, num_parents, crossover_prob, mutation_prob, use_tqdm = False):
states = []
best_solution = []
best_score = 0
if use_tqdm: pbar = tqdm(total=num_gen)
for _ in range(num_gen):
if use_tqdm: pbar.update()
# Get population fitness
scores, population = fitness_score(population)
current_best_score = scores[0]
current_best_solution = population[0]
states.append(current_best_score)
if current_best_score > best_score:
best_score = current_best_score
best_solution = int("".join(str(x) for x in copy(current_best_solution)), base=2)
parents = select_parent(population, num_parents)
parents = crossover(parents, crossover_prob)
population = mutation(population,mutation_prob)
return best_solution, best_score, states
Parameters#
# SGA Parameters
num_gen = 10000
pop_size = 5
crossover_prob = 0.7
mutation_prob = 0.3
num_parents = 2
# Solution representation
chromosome_length = 9
best_score = -100000
# Initialize the "best solution"
population = init_pop(pop_size, chromosome_length)
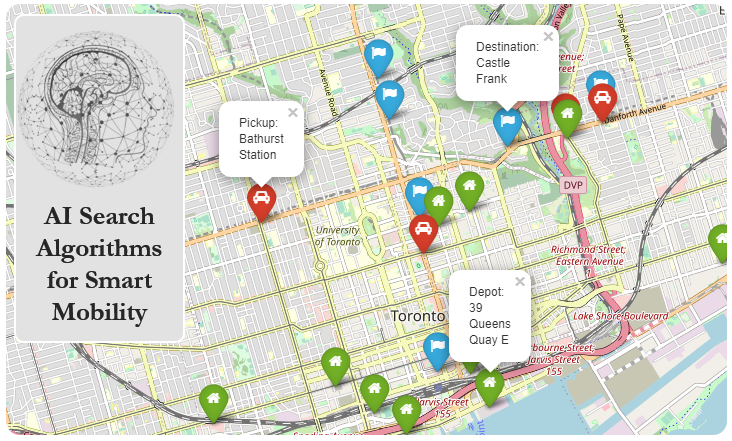
Results and Visualization#
best_solution, best_score, states = SGA(
population, num_gen, num_parents, crossover_prob, mutation_prob, use_tqdm=True
)
print(f"Best Solution: {best_solution}")
print(f"Best Score: {best_score}")
plt.plot(states)
plt.xlabel("Generations")
plt.ylabel("Cost")
plt.show()
Best Solution: 230
Best Score: 2180000.0
We can also easily verify that the solution is indeed 230, as the maximum of the profit function (solution to the derivative) is 230:
\(Profit=-200P^2+92,000P-8,400,000\)
\(\frac{dP}{dProfit}=-400P + 92000\)
Set \(\frac{dP}{dProfit}=0\)
\(400P = 92000\)
\(P=230\)
Example: Bike pricing using Real-valued Genetic Algorithm#
We can also run the above example using real-values instead. For this example, we’ll use a solver to handle the population generation, mutation, and child creation.
import numpy as np
from ypstruct import structure
import math
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Input In [10], in <cell line: 2>()
1 import numpy as np
----> 2 from ypstruct import structure
3 import math
4 import matplotlib.pyplot as plt
ModuleNotFoundError: No module named 'ypstruct'
# run Genetic Algorithm
def run(problem, params):
# Problem Information
costfunc = problem.costfunc
nvar = problem.nvar
varmin = problem.varmin
varmax = problem.varmax
# Parameters
maxit = params.maxit
npop = params.npop
beta = params.beta
pc = params.pc
nc = int(np.round(pc*npop/2)*2)
gamma = params.gamma
mu = params.mu
sigma = params.sigma
# Empty Individual Template
empty_individual = structure()
empty_individual.position = None
empty_individual.cost = None
# Best Solution Ever Found
bestsol = empty_individual.deepcopy()
bestsol.cost = np.inf
# Initialize Population
pop = empty_individual.repeat(npop)
for i in range(npop):
pop[i].position = np.random.uniform(varmin, varmax, nvar)
pop[i].cost = costfunc(pop[i].position)
if pop[i].cost < bestsol.cost:
bestsol = pop[i].deepcopy()
# Best Cost of Iterations
bestcost = np.empty(maxit)
# Main Loop
for it in tqdm(range(maxit), total=maxit):
costs = np.array([x.cost for x in pop])
avg_cost = np.mean(costs)
if avg_cost != 0:
costs = costs/avg_cost
probs = np.exp(-beta*costs)
popc = []
for _ in range(nc//2):
# Select Parents
#q = np.random.permutation(npop)
#p1 = pop[q[0]]
#p2 = pop[q[1]]
# Perform Roulette Wheel Selection
p1 = pop[roulette_wheel_selection(probs)]
p2 = pop[roulette_wheel_selection(probs)]
# Perform Crossover
c1, c2 = crossover(p1, p2, gamma)
# Perform Mutation
c1 = mutate(c1, mu, sigma)
c2 = mutate(c2, mu, sigma)
# Apply Bounds
apply_bound(c1, varmin, varmax)
apply_bound(c2, varmin, varmax)
# Evaluate First Offspring
c1.cost = costfunc(c1.position)
if c1.cost < bestsol.cost:
bestsol = c1.deepcopy()
# Evaluate Second Offspring
c2.cost = costfunc(c2.position)
if c2.cost < bestsol.cost:
bestsol = c2.deepcopy()
# Add Offsprings to popc
popc.append(c1)
popc.append(c2)
# Merge, Sort and Select
pop += popc
pop = sorted(pop, key=lambda x: x.cost)
pop = pop[0:npop]
# Store Best Cost
bestcost[it] = bestsol.cost
# Output
out = structure()
out.pop = pop
out.bestsol = bestsol
print("Best solution: ", bestsol.position)
out.bestcost = bestcost
return out
# perform single-point crossover
def crossover(p1, p2, gamma=0.1):
c1 = p1.deepcopy()
c2 = p1.deepcopy()
alpha = np.random.uniform(-gamma, 1+gamma, *c1.position.shape)
c1.position = alpha*p1.position + (1-alpha)*p2.position
c2.position = alpha*p2.position + (1-alpha)*p1.position
return c1, c2
# apply mutation
def mutate(x, mu, sigma):
y = x.deepcopy()
flag = np.random.rand(*x.position.shape) <= mu
ind = np.argwhere(flag)
y.position[ind] += sigma*np.random.randn(*ind.shape)
return y
# apply boundary constraints
def apply_bound(x, varmin, varmax):
x.position = np.maximum(x.position, varmin)
x.position = np.minimum(x.position, varmax)
# roulette wheel selection
def roulette_wheel_selection(p):
c = np.cumsum(p)
r = sum(p)*np.random.rand()
ind = np.argwhere(r <= c)
return ind[0][0]
# Fitness function
def bike_pricing(X):
return 200*math.pow(X,2) - 92000*X + 8400000
# Problem Definition
problem = structure()
problem.costfunc = bike_pricing
problem.nvar = 1
problem.varmin = [50]
problem.varmax = [350]
# Solver GA Parameters
params = structure()
params.maxit = 6000
params.npop = 5
params.beta = 1
params.pc = 1
params.gamma = 0.1
params.mu = 0.01
params.sigma = 0.1
# Run GA
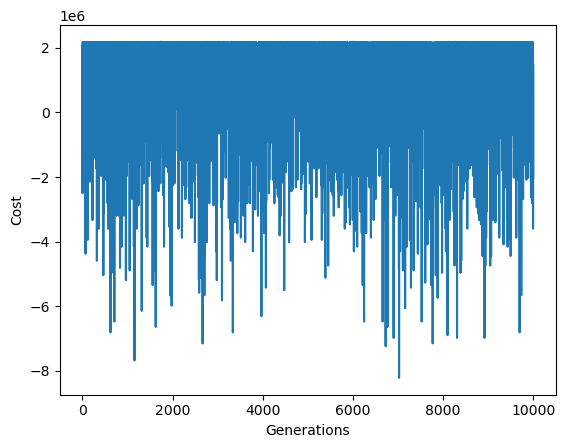
out = run(problem, params)
Best solution: [219.49875272]
# Results
plt.plot(out.bestcost)
# plt.semilogy(out.bestcost)
plt.xlim(0, params.maxit)
plt.xlabel('Iterations')
plt.ylabel('Best Cost')
plt.title('Genetic Algorithm (GA)')
plt.grid(True)
plt.show()
Example: Permutation Genetic Algorithm for TSP#
As you know by now, the Travelling Salesman Problem is essentially about generating the least costly permutation of all vertices in a graph. Assuming the graph is fully connected (every permutation is feasible), we can consider the following set of operators:
Crossover operators#
Adjacency-based operators
Partially mapped crossover
Edge crossover
Order-based operators
Order 1 crossover
Cycle crossover
Mutation Operators#
Insert mutation
Swap mutation
Inversion mutation
Scramble mutation
import networkx as nx
import matplotlib.pyplot as plt
import random
from tqdm.notebook import tqdm
from smart_mobility_utilities.common import random_tour, cost_tour
Let’s generate a random connected graph, so that any permutation of vertices is feasible.
G = nx.complete_graph(60)
for (u, v) in G.edges():
G.edges[u,v]['weight'] = random.randint(0,40)
plt.figure(figsize=(25,25))
nx.draw(G, with_labels=True)
plt.show()

Let’s assume we can generate two random tours of the graph, and we now want to generate another permutation from these two parents. We can’t simply cut and paste or swap randomly, as that will likely generate a set that is not an actual and admissible permutation. For this reason, we need to consider the following crossover types that guarantee an acceptable permutation:
Partially-mapped crossover#
This algorithm is lightweight and disrupts a lot of the genes, which is a desirable effect for GA.
def PMX_crossover(firstPermutation, secondPermutation):
# we need to know the length of either permutation
# they must be equal in size
length = len(firstPermutation)
# (1) choosing the two crossover points
# by randomly select a point from the
# first half and another point from the second half
first_Cross = random.randint(0, length // 2)
second_Cross = random.randint(length // 2 + 1, length - 1) + 1
# (2) initializing the two equal sized segments
# and create another array with the same size of
# any permutation to be the child
child = [None] * length
subP1 = firstPermutation[first_Cross:second_Cross]
subP2 = secondPermutation[first_Cross:second_Cross]
# (3) copy the elements in the segment from the first permutation
# into the same segment in the child
child[first_Cross:second_Cross] = subP1
# (4) finding common elements in the segment from the
# the first permutation and the second permutation
# and get its mirror from first permutation to second
pairs = list()
for element in subP2:
if element not in subP1:
pairs.append((element, subP1[subP2.index(element)]))
# (5) copying into the child all the elements in the segment
#. that are present in the first permutation segment but
#. aren't present in the second permutation segment.
#. if not we need to copy that element in place outside
# the segment in a place where we are sure that would
#. result into inadmissible permutations.
for pair in pairs:
second = pair[1]
if second not in subP2:
index = secondPermutation.index(second)
child[index] = pair[0]
else:
# when there is an element from the segment of the first
# permutation in the segment of the second permutation
reflect = firstPermutation[secondPermutation.index(second)]
# bouncing back and forth between the two arrays indices
# to get out of second permutation segment
while reflect in subP2:
bounce = reflect
reflect = firstPermutation[secondPermutation.index(bounce)]
child[secondPermutation.index(reflect)] = pair[0]
# (6) go through all the elements that have not been assigned
# yet in the child array and assign them with the second permutation
# elements
for i in range(length):
if child[i] == None:
child[i] = secondPermutation[i]
return child
Edge recombination crossover#
The offspring of this crossover depends on the edges and connections between nodes in each permutation.
def ERO_crossover(G, firstPermutation, secondPermutation):
# constructing edge table
edgeTable = dict()
elements = firstPermutation[:]
length = len(elements)
# just like adjacency list of nodes
# in a given graph, but it is actually
# the result of union between the two given
# adjacency lists of a certain parent from both graphs
for source in elements:
edgeTable[source] = list()
firstPermutationAdj = G[firstPermutation.index(source)]
secondPermutationAdj = G[secondPermutation.index(source)]
adjList = list(set().union(firstPermutationAdj, secondPermutationAdj))
edgeTable[source]= adjList
child = list()
parent = random.choice(elements)
elements.remove(parent)
# terminate when the length of the child is the same
# as the length of their parent
while len(child) < length:
child.append(parent)
# remove the parent from all the adjacency lists
for adjList in edgeTable.values():
try:
adjList.remove(parent)
except:
pass
parentAdjList = edgeTable[parent][:]
del edgeTable[parent]
if len(parentAdjList) == 0: continue
parent = min(parentAdjList, key = lambda parent : len(edgeTable[parent]))
return child
Order 1 crossover#
This is much simpler crossover technique. It involves copying a random segement of nodes from the first parent, and completes the child with any nodes in the second parent not already present in the child.
def ordOne_crossover(firstPermutation, secondPermutation):
length = len(firstPermutation)
# choose the start and the end of the segment
# to be copied from the first parent
start_Segment = random.randint(0, length // 2)
end_Segment = random.randint(length // 2 + 1, length - 1) + 1
# create a child
child = list()
# add the randomaly selected segment from the first parent
child.extend(firstPermutation[start_Segment: end_Segment])
# add what is left from the second parent that wasn't added from the first parent
residueFromSegment = list(set(secondPermutation) - set(firstPermutation[start_Segment: end_Segment]))
child.extend(residueFromSegment)
return child
Insert Mutation#
This mutation selects two random genes and moves the second to follow the first directly. This ensures a valid permutation.
def insert_mutation(permutation):
# copying the list so we don't mess with the original
child = permutation[:]
# choose two random genes and make sure that they are different
first_gene = random.choice(child)
second_gene = random.choice(child)
while first_gene == second_gene:
first_gene = random.choice(child)
second_gene = random.choice(child)
# removing the second gene from the list and insert it just after the first
child.remove(second_gene)
geneNewIndex = child.index(first_gene) + 1
child.insert(geneNewIndex, second_gene)
return child
Swap Mutation#
This mutation simply exchanges the positions of two nodes in a permutation.
def swap_mutation(permutation):
# copying the list so we don't mess with the original
child = permutation[:]
length = range(len(child))
# choose two random gene position so they could be swaped
first_gene_pos, second_gene_pos = random.sample(length, 2)
# swapping
child[first_gene_pos], child[second_gene_pos] =\
child[second_gene_pos], child[first_gene_pos]
return child
Implementation#
For this example, we’ll use Partially-mapped crossovers and Insert mutations, but others could be substituted as well.
# remember that ERO takes the graph as input
# not like PMX or Order 1
crossover = PMX_crossover
mutate = insert_mutation
size_of_population = 100
ngen = 500
best_at_gen = [] # for keeping track of the best tour at a given generation
# Initialize population
pool = [*random_tour(G.nodes, number_of_perms=size_of_population)]
for generation in tqdm(range(ngen)):
# 1- crossover every consecutive pair of routes
# 2- replace the weakest of the two parent with the product of the crossover
# 3- mutate the whole pool
# 4- repeat and save the value best tour in that generation
# 1-
for parent1, parent2 in zip(pool, pool[1:]):
child = crossover(parent1, parent2)
# 2-
if cost_tour(G, parent1) > cost_tour(G, parent2):
pool[pool.index(parent2)] = child
else:
pool[pool.index(parent1)] = child
# 3-
for i in range(size_of_population):
pool[i] = mutate(pool[i])
# 4-
best_at_gen.append(cost_tour(G, min(pool, key = lambda tour : cost_tour(G, tour))))
tour = min(pool, key = lambda route : cost_tour(G, route)) # result
tour_cost = cost_tour(G, tour) #result cost
plt.xlabel("number of generation")
plt.ylabel("cost of the shortest tour (meters)")
plt.plot(best_at_gen)
plt.show()
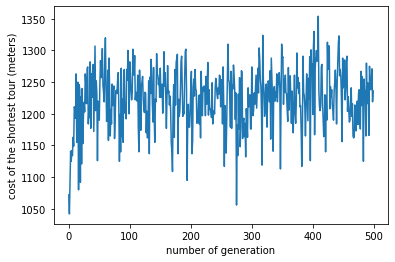
As you may notice, there is not much convergence in the costs of the tours in this GA implementation. This is largely because the solutions of the problem are very close to each other (there is only a limited range of edge weights).
Example: Permutation Genetic Algorithm for Routing Problem#
For the examples in this section, we will move past our University of Toronto search space in the previous section in favour of a more complex environment. This is the kind of network which really benefits from Genetic Search Algorithms.
Let’s consider the road network in Vaughan, a municipality to the north of Toronto:
import osmnx
G = osmnx.graph_from_address('vaughan', dist=1400)
origin = 29658954
destination = 701446851
highlighted = [origin, destination]
nc = ['r' if node in highlighted else '#336699' for node in G.nodes()]
ns = [50 if node in highlighted else 8 for node in G.nodes()]
fig, ax = osmnx.plot_graph(G, node_size=ns, node_color=nc, node_zorder=2)
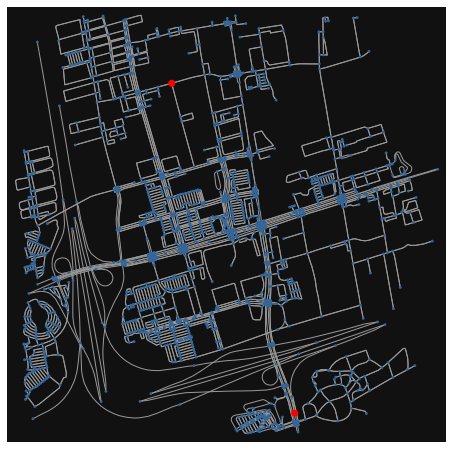
For this example, we’ll be attempting to search for the shortest route between two points highlighted in red.
The Algorithm#
There are many ways to design a genetic algorithm; the below is only one of them.
We will need a fitness function to determine which offspring to keep in each generation. This will be the length of the route generated (we want to minimize this).
As we will be doing a real-value (non-binary) GA, out phenotype is the same as our genotype.
Our GA implementation is “kind of” steady state: we probabilistically choose the best routes to be the parents of the next generation. More on this later.
We will be doing 1-point crossover.
Route mutations take place by deleting a random number of genes/nodes and trying to stitch that gap. Keep in mind this is time-intensive.
Selection is based on fitness-proportionate criteria.
The actual algorithm (in pseudo-code) looks like this:
for num_of_generations do
parents_second_gen ← crossover parents_first_gen
parents ← mutate parents_second_gen
pool ← offspring of parents
remove duplicates from pool and add random routes to compensate any removal
route ← best route in pool
return route
Mutation#
Our algorithm “mutates” a child (route) by deleting a node between two nodes in the child, and attempting to fill in the gap with alternate nodes. If you recall the way we generated “children” for Beam Search and Hill climbing in previous sections, this uses the same idea.
from smart_mobility_utilities.children import shortest_path_with_failed_nodes_single
import random
import math
def mutate(G, route):
source = route[0]
destination = route[-1]
failed = random.choice(route)
path = shortest_path_with_failed_nodes_single(G, route, [failed])
# This method could fail because of a lot of factors relating to the graph structure
# Check the documentation fo the shortest_path_with_failed_nodes to learn more
while path == math.inf:
failed = random.choice(route)
path = shortest_path_with_failed_nodes_single(G, route, [failed])
return path
Crossover#
Rather than selecting a random point to “crossover”, we look for a common node between the two routes.
import itertools
from smart_mobility_utilities.common import probability
def cross_over(route_1, route_2):
origin = route_1[0]
destination = route_1[-1]
intersection = [*itertools.filterfalse(\
lambda element : element in [origin, destination] ,\
list(set(route_1) & set(route_2)))]
if len(intersection) == 0: return route_1 # if there is not common node, just return the first route
cross_over_point = random.choice(intersection)
first_point = route_1.index(cross_over_point)
second_point = route_2.index(cross_over_point)
if probability(0.50):
return route_1[:first_point] + route_2[second_point:]
else:
return route_2[:second_point] + route_1[first_point:]
Duplicates#
Our offspring will likely result in many duplicates, as most routes will closely ressemble each other. To account for this, we remove any duplicates and replace them with new randomly generated routes. This also ensures population diversity.
The code#
from smart_mobility_utilities.common import randomized_search
# Configure some parameters
n_gen = 100 # Anything above 20 will take some time but yield much better results
pool_size = 12 # Number of routes in each generation
parents_num = 4 # needs to be a factor of pool size
# Initialize the pool
pool = [randomized_search(G,origin,destination) for _ in range(pool_size)]
# Plot the pool on a map
random_hexa = lambda: random.randint(0,255) # generate random hexadecimal color
rc = ['#%02X%02X%02X' % (random_hexa(),random_hexa(),random_hexa()) for _ in range(pool_size)]
fig, ax = osmnx.plot_graph_routes(G, pool, route_colors=rc, route_linewidth=6, node_size=0)
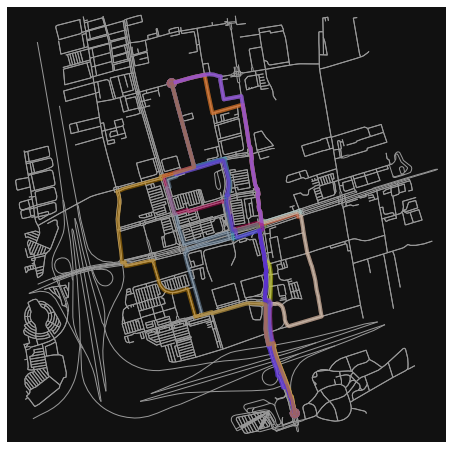
The following code will take quite a bit of time to run.
from tqdm.notebook import tqdm
from smart_mobility_utilities.common import cost, flatten
from smart_mobility_utilities.children import get_children
import heapq
states = []
def select_best(pool, num_of_choices, probability_dist):
return random.choices(population=pool, weights=probability_dist, k= num_of_choices)
for gen in tqdm(range(n_gen)):
weights = [cost(G, route) for route in pool]
parents_1 = select_best(pool, parents_num, weights)
parents_2 = [cross_over(route_1, route_2) for route_1, route_2 in itertools.combinations(parents_1, r = 2)]
pool.extend([mutate(G, route) for route in parents_2])
pool = [*map(list, list(set(map(tuple, pool))))]
num_removed = pool_size - len(pool) + 1
pool.extend([randomized_search(G, origin, destination) for _ in range(num_removed)])
pool = heapq.nsmallest(pool_size,pool,key=lambda x: cost(G,x))
m = cost(G, min(pool, key = lambda route : cost(G, route)))
states.append(m)
# Retrieve the final best route
route = min(pool, key=lambda route: cost(G,route))
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
/tmp/ipykernel_9506/2180043652.py in <module>
14 parents_1 = select_best(pool, parents_num, weights)
15 parents_2 = [cross_over(route_1, route_2) for route_1, route_2 in itertools.combinations(parents_1, r = 2)]
---> 16 pool.extend([mutate(G, route) for route in parents_2])
17 pool = [*map(list, list(set(map(tuple, pool))))]
18 num_removed = pool_size - len(pool) + 1
/tmp/ipykernel_9506/2180043652.py in <listcomp>(.0)
14 parents_1 = select_best(pool, parents_num, weights)
15 parents_2 = [cross_over(route_1, route_2) for route_1, route_2 in itertools.combinations(parents_1, r = 2)]
---> 16 pool.extend([mutate(G, route) for route in parents_2])
17 pool = [*map(list, list(set(map(tuple, pool))))]
18 num_removed = pool_size - len(pool) + 1
/tmp/ipykernel_9506/672098679.py in mutate(G, route)
9 failed = random.choice(route)
10
---> 11 path = shortest_path_with_failed_nodes_single(G, route, [failed])
12
13 # This method could fail because of a lot of factors relating to the graph structure
~/book-env/smart_mobility_utilities/smart_mobility_utilities/children.py in shortest_path_with_failed_nodes_single(G, route, failed)
9 i = 1
10 j = len(route) -2
---> 11 result = shortest_path_with_failed_nodes(G,route,i,j,failed)
12 if result is math.inf: return result
13 path, i,j, r = result
~/book-env/smart_mobility_utilities/smart_mobility_utilities/children.py in shortest_path_with_failed_nodes(G, route, i, j, failed)
47
48 while len(unrelaxed_nodes) > 0:
---> 49 node = min(unrelaxed_nodes, key = lambda node : shortest_dist[node])
50
51 # if we have relaxed articulation nodes in our graph
~/book-env/smart_mobility_utilities/smart_mobility_utilities/children.py in <lambda>(node)
47
48 while len(unrelaxed_nodes) > 0:
---> 49 node = min(unrelaxed_nodes, key = lambda node : shortest_dist[node])
50
51 # if we have relaxed articulation nodes in our graph
~/book-env/smart_mobility_utilities/smart_mobility_utilities/common.py in __eq__(self, other)
57 return self.osmid == other.osmid
58 except:
---> 59 return self.osmid == other
60
61
KeyboardInterrupt:
from smart_mobility_utilities.viz import draw_route
import matplotlib.pyplot as plt
print("Cost of the route:",cost(G,route))
ax = plt.plot(states)
draw_route(G,route, zoom=13)