Tabu Search#
Tabu search (TS) is an iterative neighborhood search algorithm, where the neighborhood changes dynamically. TS enhances local search by actively avoiding points in the search space already visited. By avoiding already visited points, loops in search trajectories are avoided and local optima can be escaped. TS can be considered as the combination of local search (LS) and memory structures. The main feature of TS is the use of an explicit memory. Uses of memory have two goals: to prevent the search from revisiting previously visited solutions and to explore the unvisited areas of the solution space.
TABU-SEARCH(graph,source,destination) return a route
best_solution ← initial random solution
best_solution_cost ← cost(best_solution)
tabu_history ← best_solution
num_iterations ← number of iterations // this is required to terminate the algorithm
tabu_limit ← number of iterations before a tabu entry is "forgotten"
tabu_size ← maximum length of tabu_history
for i to num_iterations do
best_solution_cost ← cost(best_solution)
tabu_history ← best_solution
num_iterations ← number of iterations // this is required to terminate the algorithm
tabu_limit ← number of iterations before a tabu entry is "forgotten"
tabu_size ← maximum length of tabu_history
for i to num_iterations do
reduce all entries in tabu_history by 1
candidates ← neighbouring solutions of best_solution
for candidate in candidates do
tabu_history ← best_candidate
if tabu_history.size > tabu_size then
candidates ← neighbouring solutions of best_solution
for candidate in candidates do
if candidate in tabu_history then
remove candidate from candidates
best_candidate ← best solution in candidatesremove candidate from candidates
tabu_history ← best_candidate
if tabu_history.size > tabu_size then
trim tabu_history until within tabu_size
for item in tabu_history do
if item < tabu_limit then
tabu_history.pop(item)
Essentially, neighbouring solutions are found for the initial randomized solution. The best solution is selected, and is added to a tabu list. For future iterations, tabu items are disqualified as potential candidates, unless enough time has passed and they can be reconsidered. This prevents the tabu search from getting stuck at a local minimum.
Additionally, an aspiration criteria can be used to prematurely “free up” a tabu item and renew it for consideration.
Example: Tabu Search for TSP#
# Initialize the graph
import networkx as nx
import random
import matplotlib.pyplot as plt
import math
G = nx.complete_graph(25)
for (u,v) in G.edges():
G.edges[u,v]['weight'] = random.randint(0,10)
plt.figure(figsize=(25,25))
nx.draw(G, with_labels=True)
plt.show()
# Define a function to calculate the tour cost
def cost_of_tour(G, tour):
cost = 0
for u, v in zip(tour, tour[1:]):
cost += G[u][v]["weight"]
cost += G[len(tour) - 1][0]["weight"]
return cost
def get_best_neighbour(G, tour, tabu_history, tabu_limit, aspiration):
best_neighbour = None
best_neighbour_cost = math.inf
# generate a list of all possible neighbours
# a neighbour is just swapping the position of two nodes within the tour
for i in range(len(G.nodes)):
for j in range(len(G.nodes)):
if i == j:
continue
# Swap the ith and jth nodes
tmp_route = tour.copy()
tmp = tmp_route[i]
tmp_route[i] = tmp_route[j]
tmp_route[j] = tmp
tmp_cost = cost_of_tour(G, tmp_route)
# This route is tabu, check aspiration
if tuple(tmp_route) in tabu_history:
if tabu_history[tuple(tmp_route)] > 0:
if tabu_history[tuple(tmp_route)] > aspiration:
continue
if tmp_cost < best_neighbour_cost:
best_neighbour_cost = tmp_cost
best_neighbour = tmp_route
tabu_history[tuple(best_neighbour)] = tabu_limit
return best_neighbour
def tabu_search(
G,
initial_solution,
num_iter,
tabu_history,
tabu_limit,
aspiration,
cost_function,
neighbour_function,
use_historical_best=False,
use_tqdm = False
):
best_solution = initial_solution
historical_best = best_solution
historical_best_cost = cost_function(G,historical_best)
best_cost = cost_function(G, best_solution)
states = [best_cost]
if use_tqdm:
pbar = tqdm(total=num_iter)
for _ in range(num_iter):
# Reduce counter for all tabu
if use_tqdm: pbar.update()
for x in tabu_history:
tabu_history[x] -= 1
tabu_history = {x: tabu_history[x] for x in tabu_history if tabu_history[x] > 0}
best_solution = neighbour_function(
G, best_solution, tabu_history, tabu_limit, aspiration
)
best_cost = cost_function(G, best_solution)
if best_cost <= historical_best_cost:
historical_best = best_solution
historical_best_cost = best_cost
states.append(best_cost)
return best_solution, best_cost, states
# Initialize some parameters
aspiration = 2
tabu_history = {}
num_iterations = 100
tabu_limit = 5
# Initialize a random solution, and its cost
initial_solution = [*G.nodes()]
random.shuffle(initial_solution)
initial_cost = cost_of_tour(G, initial_solution)
print(f"Initial solution: {initial_solution}")
print(f"Initial cost: {initial_cost}")
best_solution, best_cost, states = tabu_search(
G,
initial_solution,
num_iterations,
tabu_history,
tabu_limit,
aspiration,
cost_of_tour,
get_best_neighbour,
)
print(f"Best Solution: {best_solution}")
print(f"Best Cost: {best_cost}")
plt.xlabel("# Iterations")
plt.ylabel("Cost")
plt.plot(states)
plt.show()
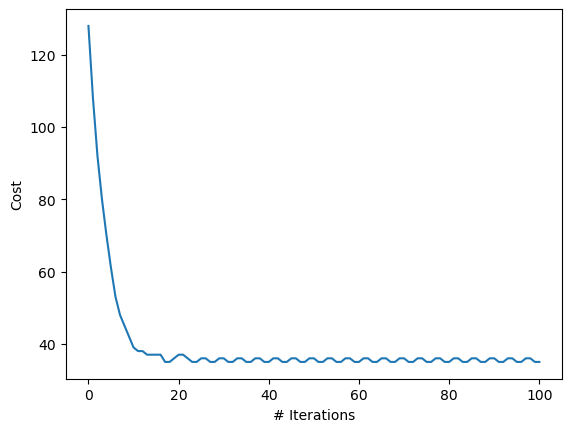
Initial solution: [3, 23, 1, 4, 20, 7, 19, 6, 16, 18, 14, 13, 12, 5, 15, 0, 2, 21, 11, 22, 17, 9, 24, 10, 8]
Initial cost: 128
Best Solution: [23, 4, 9, 13, 20, 0, 6, 19, 14, 15, 1, 5, 12, 11, 18, 3, 8, 21, 7, 22, 24, 16, 17, 10, 2]
Best Cost: 35
Example: Tabu Search for Routing Problem#
We can also use Tabu Search for our University of Toronto routing problem, however we will need to define some new functions.
# Setup the Graph, origin, and destination
import osmnx
from smart_mobility_utilities.common import Node, randomized_search, cost
from smart_mobility_utilities.viz import draw_route, draw_map
reference = (43.661667, -79.395)
G = osmnx.graph_from_point(reference, dist=300, clean_periphery=True, simplify=True)
origin = Node(graph=G, osmid=389677909)
destination = Node(graph=G, osmid=55808290)
highlighted = [389677909, 55808290]
# marking both the source and destination node
nc = ["red" if node in highlighted else "#336699" for node in G.nodes()]
ns = [50 if node in highlighted else 8 for node in G.nodes()]
fig, ax = osmnx.plot_graph(G, node_size=ns, node_color=nc, node_zorder=2)
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Input In [6], in <cell line: 3>()
1 # Setup the Graph, origin, and destination
2 import osmnx
----> 3 from smart_mobility_utilities.common import Node, randomized_search, cost
4 from smart_mobility_utilities.viz import draw_route, draw_map
6 reference = (43.661667, -79.395)
ModuleNotFoundError: No module named 'smart_mobility_utilities'
from smart_mobility_utilities.children import get_children
from tqdm.notebook import tqdm
def get_best_neighbour_route(G, route, tabu_history, tabu_limit, aspiration):
best_neighbour = route
best_neighbour_cost = math.inf
# generate a list of neighbours, disable multiprocessing if unavailable
neighbours = get_children(G, route,num_children=-1,multiprocessing=True,workers=4)
for child in neighbours:
child_cost = cost(G,child)
# This route is tabu, check aspiration
if tuple(child) in tabu_history:
if tabu_history[tuple(child)] > aspiration:
continue
if child_cost < best_neighbour_cost:
best_neighbour_cost = child_cost
best_neighbour = child
tabu_history[tuple(best_neighbour)] = tabu_limit
return best_neighbour
# Initialize some parameters
aspiration = 2
tabu_history = {}
num_iterations = 50
tabu_limit = 10
# Initialize a random solution, and its cost
initial_solution = randomized_search(G, origin.osmid, destination.osmid)
initial_cost = cost(G,initial_solution)
print(f"Initial Solution: {initial_solution}")
print(f"Initial Cost: {initial_cost}")
best_solution, best_cost, states = tabu_search(
G,
initial_solution,
num_iterations,
tabu_history,
tabu_limit,
aspiration,
cost,
get_best_neighbour_route,
use_historical_best=True,
use_tqdm=True
)
Initial Solution: [389677909, 389678133, 2557539841, 389678131, 6028561921, 6028561924, 24960080, 3707407641, 249991437, 24960070, 389678145, 1258698109, 24960068, 9270977978, 389678104, 9270977960, 389678267, 9270977966, 3179025274, 9270977970, 55808169, 55808177, 55808290]
Initial Cost: 909.173
print(f"Best Solution: {best_solution}")
print(f"Best Cost: {best_cost}")
draw_route(G,best_solution)
Best Solution: [389677909, 749952029, 389677908, 854322047, 6028562356, 389678131, 5098988924, 6028561924, 24960080, 3707407641, 249991437, 24960070, 389678145, 1258698109, 24960068, 9270977978, 24960090, 3108569783, 9270977966, 3179025274, 9270977970, 1721866234, 304891685, 55808290]
Best Cost: 821.922
plt.xlabel("# Iterations")
plt.ylabel("Cost")
plt.plot(states)
plt.show()
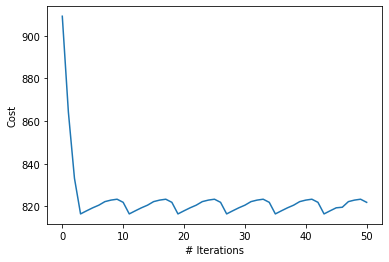
As you may notice, the results above show that the search algorithm was stuck in a cycle. This is because the neighbourhood space of the routes are limited, of which only a very small subset are solutions that would actually generate a “better” cost. To counteract this, we can keep track of the “historically” best solution, and choose this as the best solution at the end of the run.
Recall the Search Comparison results from a previous section; compared to the 801.64 result from Dijkstra, this method produces non-optimal but still “pretty good” results.