Ant Colony Optimization

Ant colony optimization is a class of optimization algorithm that uses a probabilistic way of finding shortest paths. It seeks to replicate the behaviour of real-world ant navigation, where ants leave pheremones when returning from food-gathering trips.

Because these pheremones evaporate over time, shorter paths tend to maintain stronger pheremone traces, and thus are favoured by outbound ants looking for food. As more and more ants use these shorter paths, the pheremone trace becomes stronger. This produces a reinforcing effect favouring optimal solutions.

Let’s revisit our University of Toronto search space.

import osmnx
from smart_mobility_utilities.common import Node, cost
from smart_mobility_utilities.viz import draw_route
import random
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt

reference = (43.661667, -79.395)

G = osmnx.graph_from_point(reference, dist=300, clean_periphery=True, simplify=True)

origin = Node(graph=G, osmid=55808290)
destination = Node(graph=G, osmid=389677909)

highlighted = [389677909, 55808290]

# marking both the source and destination node

nc = ['red' if node in highlighted else '#336699' for node in G.nodes()]
ns = [50 if node in highlighted else 8 for node in G.nodes()]
fig, ax = osmnx.plot_graph(G, node_size=ns, node_color=nc, node_zorder=2)

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [1], in <cell line: 2>()
      1 import osmnx
----> 2 from smart_mobility_utilities.common import Node, cost
      3 from smart_mobility_utilities.viz import draw_route
      4 import random

ModuleNotFoundError: No module named 'smart_mobility_utilities'

Our Ant Colony algorithm will follow these steps:

1. We generate \(n\) number of ants to fill our population, and place them all at the origin point (the colony).

2. We initialize the pheromone concentrations to random values, to seed the graph.

3. For each ant, the following procedures are followed:

   • The ant examines all the edges leading to neighbouring nodes, and probabilistically chooses an edge to travel based on pheromone levels. If one of the neighbouring nodes is the destination (the food source), the ant overrides this probability and goes straight for the destination.

   • If the ant is stuck, it retraces its steps back to a previous node with unexplored neighbours.

   • The ant now retraces its route, and deposits pheromone on the route, weighted inversely to the edge length.

   • If the route is a newly discovered route, we add it to our list of all known routes.

4. The route that is most frequented by the ants is selected as the “best” solution.

# Initialize the parameter

# Alpha and Beta are used in the pheremone calculation
alpha = 2
beta = 2

n = 500
Q = 1 # factor for post-route pheremone increase

pheremone_concentrations = dict()
known_routes = dict()

# randomize the pheromones
pheremone_concentrations = {(u,v):random.uniform(0,0.5) for [u,v] in G.edges()}

# a function to calculate pheremone levels
def pheremone(level, distance, alpha, beta):
    return level ** alpha * ((1/distance)) ** beta

for ant in tqdm(range(n)):
    # Place the ant at the colony
    frontier = [origin]
    explored = set()
    route = []
    found = False

    while frontier and not found:
        parent = frontier.pop(0)
        explored.add(parent)

        children = []
        children_pheremones = []
        for child in parent.expand():
            # If we see the destination, ignore all pheremones
            if child == destination:
                found = True
                route = child.path()
                continue
            if child not in explored:
                children.append(child)
                children_pheremones.append(
                    pheremone(
                        pheremone_concentrations[(parent.osmid, child.osmid)],
                        child.distance,
                        alpha,
                        beta,
                    )
                )

        if len(children) == 0:
            continue  # The ant is stuck, go back.

        transition_probability = [
            children_pheremones[i] / sum(children_pheremones)
            for i in range(len(children_pheremones))
        ]

        # Probabilistically choose a child to explore based weighted by transition probability
        chosen = random.choices(children, weights=transition_probability, k=1)[0]

        # Add all the non-explored children in case we need to explore them later
        children.pop(children.index(chosen))
        frontier.extend(children)

        # Set the chosen child to be the next node to explore
        frontier.insert(0, chosen)
    
    # We now have a completed route, we can increase pheremone levels 
    # on that route for the next ant to detect.

    for u, v in zip(route[:-1], route[1:]):
        length_of_edge = G[u][v][0]['length']
        pheremone_concentrations[(u,v)] += Q/length_of_edge
    
    # If the route is newly discovered, add it to the list
    route = tuple(route)
    if route in known_routes:
        known_routes[route] += 1
    else:
        known_routes[route] = 1

best_route = max(known_routes, key=known_routes.get)
times_used = known_routes[best_route]

route = list(best_route)
print("Cost:", cost(G,route))
print("Times used:",times_used)
draw_route(G,route)

Cost: 927.453
Times used: 325

costs = [cost(G,r) for r in known_routes]
used = list(known_routes.values())

costs, used = zip(*sorted(zip(costs,used)))

plt.plot(costs, used)
plt.xlabel('Solution cost')
plt.ylabel('Times travelled')
plt.show()

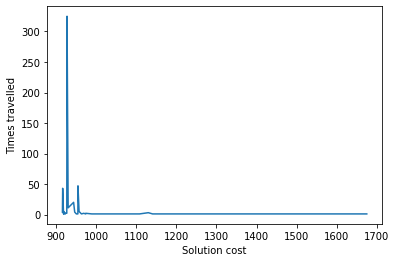
As we can see, the most travelled route has a lower cost, as the pheremones from that route are reinforced by each subsequent ant.