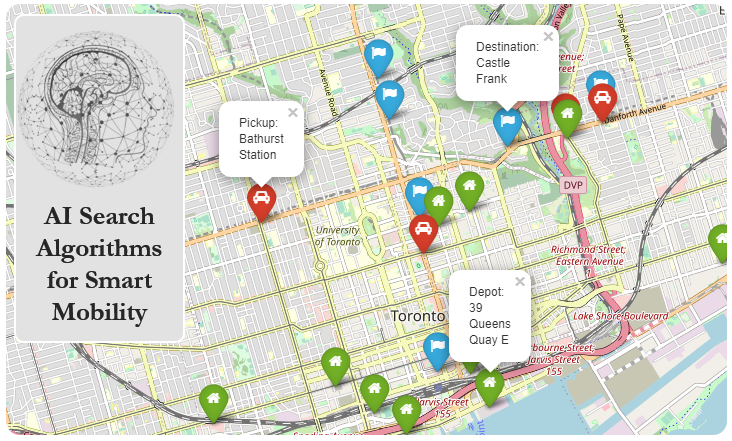
Trip Itinerary Planning#
Authors: Jingkai Jia, Yuli Chen and Yuxuan Liu
Course: ECE1724H: Bio-inspired Algorithms for Smart Mobility - Fall 2021
Instructor: Dr. Alaa Khamis
Department: Edward S. Rogers Sr. Department of Electrical & Computer Engineering, University of Toronto
Introduction#
The Trip Itinerary Problem (TIP) consists of a problem where a list of locations to visit must be selected, and have routes formulated between them, such that some sort of cost function (such as number of visited places, POI ranking, traveller satisfaction, etc) is maximized.
Essentially, the problem can be broken down into the following:
Select a subset from a set of POIs (or candidate points).
Construct one or more routes between a home point (like a hotel, etc.) and those points, in order to satisfy time and distance constraints.
from ipyleaflet import AntPath,Map,Marker
from ipywidgets import HTML
import osmnx as ox
import pandas as pd
import numpy as np
import os
import requests
import json
import random
import time
import folium
import folium.plugins
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
from collections import OrderedDict
from itertools import combinations
from smart_mobility_utilities.poi import number_DivIcon
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Input In [1], in <cell line: 17>()
15 from collections import OrderedDict
16 from itertools import combinations
---> 17 from smart_mobility_utilities.poi import number_DivIcon
ModuleNotFoundError: No module named 'smart_mobility_utilities'
Dataset#
This implementation uses a dataset compiled from a public source listing POIs and Attractions in Toronto, supplemented with further data from mapping APIs such as Google Maps API.
A total of 165 POIs exist in the dataset.
Additionally, a precomputed matrix of distances between POIs was created in order eliminate the need for real-time distance queries and speed up the algorithm running times.
Problem Formulation#
Variables#
\(V_i\) : poi i
\(R_i\) : rating of \(V_i\)
\(C_{ij}\) : the time it takes for the user to travel from \(V_i\) to \(V_j\)
\(L_{ij}\) : the distance between \(V_i\) and \(V_j\)
\(O_i,E_i\) : the openning/closing time of \(V_i\)
\(D_i\) : duration visitor want to spend on \(V_i\)
\(S_i\) : the time when the visitor arrives \(V_i\)
\(a_{ijk}\) : whether \(V_j\) is visited after \(V_i\) in tour \(k\). True -> 1, False -> 0
\(b_{ij}\) : whether \(V_i\) is visited in tour \(j\). True -> 1, False -> 0
\(m\) : the number of tours a visitor wants to take
\(\gamma\) : weight of soft constraint
\( T_{start}, T_{end}\) : start and end time of the tour
\(Q\) : a large positive constant used for integer programming modelling
Objective#
\(\sum_{i=0}^{m} \sum_{j=1}^{n} R_i b_{ij} - \sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{k=1}^{m} \gamma L_{ij} a_{ijk}\)
Constraints#
\(\sum_{i=0}^{m} \sum_{j=1}^{n} a_{1ij} = \sum_{i=0}^{m} \sum_{j=1}^{n} a_{nij} = m\) (m tours are start from V1 and end with Vn)
\(\sum_{i=2}^{n-1} \sum_{j=1}^{m} b_{ij} \le 1\) (all vertices are visited only once)
\(\sum_{i=1}^{n-1} a_{ijk} = b_{kj}, k=2,...,n-1; j=1,...,m\) (all tours are connected, used together with the constraint below)
\(\sum_{i=2}^{n} a_{ijk} = b_{kj}, k=2,...,n-1; j=1,...,m\) (all tours are connected, used together with the constraint above)
\(S_{ik} + D_{i} + C_{ij} - S_{jk} \le Q(1-a_{ijk}), \> i=1,...,n-1;j = 2,... n; k = 1,...,m\) (travel time is continuous)
\(O_{i} \le S_{ij} + D_{i} \le E_{i}, \> i = 1,...,n; j = 1,...,m\) (vertices are visited within the time window)
Data Object#
The following class stores information about POIs, as well as loads POI distance information from the precomputed matrix.
class POI:
def __init__(self, name, id, category, lat, lng, rating=None, openings=None):
self.name = name
self.id = id
self.category = category
self.coordinates = (lat,lng)
if np.isnan(lat) or np.isnan(lng):
self.coordinates = (0,0)
self.rating = rating
self.visit_duration = 100.0
self.open_time, self.close_time = openings
self.open_time = self.open_time // 100 * 60 + self.open_time % 100
self.close_time = self.close_time // 100 * 60 + self.close_time % 100
self.BASE_DIR = ""
self.route_cache = dict()
self.min_duration = float('inf')
if self.id >= 0:
self.warm_cache()
def warm_cache(self):
from_id = int(self.id)
df = pd.read_csv('{}cache/poi_pair_cost_{}.csv'.format(self.BASE_DIR, from_id))
with open('cache/coords_db_{}.json'.format(from_id)) as f:
coord_db = json.loads(f.read())
for index, row in df.iterrows():
result = {
'coords': None,
'length': None,
'duration': None
}
to_id = int(row['to_id'])
result['duration'] = float(row['duration']) / 60.0
self.min_duration = min(self.min_duration, result['duration'])
result['length'] = float(row['length'])
result['coords'] = coord_db[str(from_id)][str(to_id)]
self.route_cache[(from_id, to_id)] = result
def query_route_db(self, from_id, to_id):
if (from_id, to_id) not in self.route_cache:
result = {
'coords': None,
'length': None,
'duration': None
}
df = pd.read_csv('{}cache/poi_pair_cost_{}.csv'.format(self.BASE_DIR, from_id))
result['duration'] = float(df[ df['to_id'] == to_id ]['duration']) / 60.0
result['length'] = float(df[ df['to_id'] == to_id ]['length'])
with open('cache/coords_db_{}.json'.format(from_id)) as f:
result['coords'] = json.loads(f.read())[str(from_id)][str(to_id)]
self.route_cache[(from_id, to_id)] = result
else:
result = self.route_cache[(from_id, to_id)]
return result
def route_to(self, destination, mode = "driving"):
from_id = self.id
to_id = destination.id
try:
result = self.query_route_db(from_id, to_id)
except:
print(from_id, to_id)
raise
return result
def __eq__(self, other):
return self.id == other.id
def __hash__(self):
return self.id
def __repr__(self):
return f"ID: {self.id}, Name: {self.name}, Score: {self.rating}"
def get_pois(file):
df = pd.read_csv(file)
my_pois = []
for i, row in df.iterrows():
name,category,geoid,lat,lng,rating,openings,closings = row.values.tolist()
poi = POI(name, i, category, lng, lat , rating, (openings, closings))
my_pois.append(poi)
return my_pois
def getRouteBounds(tours):
for tour in tours:
route = [ (t.coordinates[1], t.coordinates[0]) for t in tour]
minLat = min(route, key=lambda x:x[0])
maxLat = max(route, key=lambda x:x[0])
minLng = min(route, key=lambda x:x[1])
maxLng = max(route, key=lambda x:x[1])
return [(minLat, minLng), (maxLat, maxLng)]
Problem Class#
class Problem:
def __init__(self, use_soft_constraint=False, alpha=1e-5, number_of_tour=2):
self.pois = get_pois('pois.csv')
self.home_poi = POI('Home', 166, 'HOME', -79.3969, 43.6596, rating=0, openings=(900, 1700))
self.number_of_tour = number_of_tour
self.id_pois_map = { poi.id: poi for poi in self.pois}
self.evaluation_cache = {}
for i in range(self.number_of_tour-1):
self.id_pois_map[-(i+1)] = POI('Spliter', -(i+1), 'SPL', 0,0, rating=0, openings=(0, 0))
self.use_evaluation_cache = True
# if use soft constraint, we apply some penalty to the evaluation function wrt the length driving
self.use_soft_constraint = use_soft_constraint
self.alpha = alpha
self.min_duration = [poi.min_duration for poi in self.pois]
def reset(self):
use_soft_constraint = self.use_soft_constraint
alpha = self.alpha
number_of_tour = self.number_of_tour
self.__init__(use_soft_constraint, alpha, number_of_tour)
def navie_decode(self, gaint_tour):
'''
split a gaint tour into a list of single tour
with out feasibility check
example
>> a = [1,3,-1,2,4]
>> b = naive_decode(a)
>> b # 5 is the id for home
[ [5, 1, 3, 5],
[5, 2, 4, 5] ]
'''
solution = []
tour = []
gaint_tour = [self.home_poi] + gaint_tour
for poi in gaint_tour:
if poi.id < 0:
tour.append(self.home_poi)
solution.append(tour)
tour = [self.home_poi]
else:
tour.append(poi)
solution.append(tour)
solution[-1].append(self.home_poi)
return solution
def can_visit(self, current_time, current_poi, next_poi):
if current_time + current_poi.route_to(next_poi)['duration'] + next_poi.visit_duration> next_poi.close_time:
return False
tentative_arrive_time = max(next_poi.open_time, current_time + current_poi.route_to(next_poi)['duration'])
tentative_leave_time = tentative_arrive_time + next_poi.visit_duration
earliest_back_home_time = tentative_leave_time + next_poi.route_to(self.home_poi)['duration']
if earliest_back_home_time > self.home_poi.close_time:
return False
return True
def filter_infeasible_pois(self, tour):
current_time = None
feasible_tour = []
for i, next_poi in enumerate(tour):
if i == 0:
current_time = next_poi.open_time
current_poi = next_poi
feasible_tour.append(current_poi)
continue
if next_poi == self.home_poi:
feasible_tour.append(self.home_poi)
break
if self.can_visit(current_time, current_poi, next_poi):
current_time = max(next_poi.open_time, current_time + current_poi.route_to(next_poi)['duration']) + next_poi.visit_duration
current_poi = next_poi
feasible_tour.append(current_poi)
return feasible_tour
def build_feasible_solution(self, solution):
feasible_soluion = []
for tour in solution:
feasible_tour = self.filter_infeasible_pois(tour)
feasible_soluion.append(feasible_tour)
return feasible_soluion
def gaint_tour_decode(self, gaint_tour):
infeasible_solution = self.navie_decode(gaint_tour)
feasible_solution = self.build_feasible_solution(infeasible_solution)
return feasible_solution
def get_initial_soluton(self, mode='random'):
if mode == 'random':
gaint_tour = random.sample([poi.id for poi in self.pois], len(self.pois))
for i in range(self.number_of_tour - 1):
gaint_tour.insert(random.randrange(len(gaint_tour)+1), -(i+1))
return gaint_tour
def evaluate(self, gaint_tour):
if self.use_evaluation_cache and tuple(gaint_tour) in self.evaluation_cache:
return self.evaluation_cache[tuple(gaint_tour)]
gaint_poi_tour = [self.id_pois_map[i] for i in gaint_tour]
solution = self.gaint_tour_decode(gaint_poi_tour)
score = 0.0
for tour in solution:
for poi in tour:
score += poi.rating
if self.use_soft_constraint:
score -= self.alpha * (self.get_tour_length(tour))
if self.use_evaluation_cache and tuple(gaint_tour) not in self.evaluation_cache:
self.evaluation_cache[tuple(gaint_tour)] = score
return score
@staticmethod
def draw_tours(tours):
center = [43.6596,-79.3969]
m = folium.Map(zoom_start = 12)
bounds = getRouteBounds(tours)
m.fit_bounds(bounds)
color_set = ['yellow','green','red','blue']
for tour in tours:
tour_route = []
color = color_set.pop()
i = 1
for u,v in zip(tour[0:],tour[1:]):
if i == len(tour) - 1:
i = 0
folium.Marker(location=list(v.coordinates)[::-1], icon=folium.Icon(color='white', icon_color='white')).add_to(m)
folium.Marker(location=list(v.coordinates)[::-1], icon=number_DivIcon(color,i)).add_to(m)
r = u.route_to(v)['coords']
tour_route += r
i += 1
ant_path = folium.plugins.AntPath(
locations=[
tour_route
],
dash_array=[1, 10],
delay=1000,
color=color,
)
ant_path.add_to(m)
return m
@staticmethod
def get_tour_length(tour):
length = 0
for u,v in zip(tour[0:],tour[1:]):
if u != v:
length += u.route_to(v)['length']
return length
GA Solver#
A solution class for Genetic Algorithm
class GeneticAlgorithmSolver:
def __init__(self, population_size=20):
self.global_solution = None
self.global_score = float('-inf')
self.max_geneartions = 1000
self.population = []
self.population_size = population_size
self.problem = None
self.mutation_prob = 0.1
self.crossover_prob = 0.7
self.adaptive = False
self.converge_threshold = 0.1
self.fitness_level = 1.0
self.score_history = []
self.converge_history = []
self.terminate_threshold = float('-inf')
def reset(self):
population_size = self.population_size
self.__init__(population_size)
def update_global(self, score, solution):
if score > self.global_score:
self.global_solution = solution
self.global_score = score
def pmx(self, a, b):
c = [None] * len(a)
start = random.randint(0, len(a)//2 - 1)
kept_idx = set([i for i in range(start, start+len(a)//2)])
kept_val = {a[i] for i in kept_idx}
for i in kept_idx:
c[i] = a[i]
if b[i] in kept_val:
continue
val = a[i]
j = b.index(val)
while j in kept_idx:
val = a[j]
j = b.index(val)
c[j] = b[i]
for i in range(len(c)):
if c[i] is None:
c[i] = b[i]
return c
def permutation_cross_over(self, a, b, mode='pmx'):
if mode == 'pmx':
child = self.pmx(a, b)
return child
def mutate(self, individual):
if self.adaptive:
mutation_prob = self.mutation_prob * ( 1.0 / (self.fitness_level + 1e-2) )
else:
mutation_prob = self.mutation_prob
if mutation_prob > np.random.uniform():
for i in range( int( 1 + 1.0 / (self.fitness_level + 1e-2) ) ):
idx = range(len(individual))
c1, c2 = random.sample(idx, 2)
individual[c1], individual[c2] = individual[c2], individual[c1]
return individual
def generate_next(self, population):
next_generation = population[:]
for i in range(10):
if len(population) <= 2:
break
if self.crossover_prob > np.random.uniform():
parent_a = population.pop(random.randrange(0, len(population)))
parent_b = population.pop(random.randrange(0, len(population)))
child = self.permutation_cross_over(parent_a, parent_b)
child = self.mutate(child)
next_generation.append(child)
return next_generation
def select(self, population):
score_board = []
for individual in population:
score = self.problem.evaluate(individual)
self.update_global(score, individual)
score_board.append( [score, individual] )
score_board.sort(key=lambda x: x[0], reverse=True)
scores = [x[0] for x in score_board]
score_board = [x[1] for x in score_board]
self.converge_history.append(np.average(scores[:self.population_size]))
next_gen = score_board[:self.population_size]
if self.adaptive and np.var(scores) < self.converge_threshold:
for i in range(self.population_size//2, self.population_size):
random.shuffle(next_gen[i])
if self.adaptive:
self.fitness_level = np.var(scores)
return next_gen
def solve(self, problem):
self.problem = problem
for _ in range(self.population_size):
individual = problem.get_initial_soluton()
score = problem.evaluate(individual)
self.update_global( score, individual)
self.population.append(individual)
for geneartion in tqdm(range(self.max_geneartions)):
next_population_candidates = self.generate_next(self.population)
self.population = self.select(next_population_candidates)
self.score_history.append(self.global_score)
return geneartion
Adaptive GA Solver#
Adaptive variant of GA Solver
import numpy as np
class AdaptiveGeneticAlgorithmSolver:
def __init__(self, population_size=20):
self.global_solution = None
self.global_score = float('-inf')
self.max_geneartions = 1000
self.population = []
self.population_size = population_size
self.problem = None
self.mutation_prob = 0.1
self.crossover_prob = 0.7
self.adaptive = True
self.converge_threshold = 0.1
self.fitness_level = 1.0
self.score_history = []
self.converge_history = []
self.terminate_threshold = float('-inf')
def reset(self):
population_size = self.population_size
self.__init__(population_size)
def update_global(self, score, solution):
if score > self.global_score:
self.global_solution = solution
self.global_score = score
def pmx(self, a, b):
c = [None] * len(a)
start = random.randint(0, len(a)//2 - 1)
kept_idx = set([i for i in range(start, start+len(a)//2)])
kept_val = {a[i] for i in kept_idx}
for i in kept_idx:
c[i] = a[i]
if b[i] in kept_val:
continue
val = a[i]
j = b.index(val)
while j in kept_idx:
val = a[j]
j = b.index(val)
c[j] = b[i]
for i in range(len(c)):
if c[i] is None:
c[i] = b[i]
return c
def permutation_cross_over(self, a, b, mode='pmx'):
if mode == 'pmx':
child = self.pmx(a, b)
return child
def mutate(self, individual):
if self.adaptive:
mutation_prob = self.mutation_prob * ( 1.0 / (self.fitness_level + 1e-2) )
else:
mutation_prob = self.mutation_prob
if mutation_prob > np.random.uniform():
for i in range( int( 1 + 1.0 / (self.fitness_level + 1e-2) ) ):
idx = range(len(individual))
c1, c2 = random.sample(idx, 2)
individual[c1], individual[c2] = individual[c2], individual[c1]
return individual
def generate_next(self, population):
next_generation = population[:]
for i in range(10):
if len(population) <= 2:
break
if self.crossover_prob > np.random.uniform():
parent_a = population.pop(random.randrange(0, len(population)))
parent_b = population.pop(random.randrange(0, len(population)))
child = self.permutation_cross_over(parent_a, parent_b)
child = self.mutate(child)
next_generation.append(child)
return next_generation
def select(self, population):
score_board = []
for individual in population:
score = self.problem.evaluate(individual)
self.update_global(score, individual)
score_board.append( [score, individual] )
score_board.sort(key=lambda x: x[0], reverse=True)
scores = [x[0] for x in score_board]
score_board = [x[1] for x in score_board]
self.converge_history.append(np.average(scores[:self.population_size]))
next_gen = score_board[:self.population_size]
if self.adaptive and np.var(scores) < self.converge_threshold:
for i in range(self.population_size//2, self.population_size):
random.shuffle(next_gen[i])
if self.adaptive:
self.fitness_level = np.var(scores)
return next_gen
def solve(self, problem):
self.problem = problem
for _ in range(self.population_size):
individual = problem.get_initial_soluton()
score = problem.evaluate(individual)
self.update_global( score, individual)
self.population.append(individual)
for geneartion in tqdm(range(self.max_geneartions)):
next_population_candidates = self.generate_next(self.population)
self.population = self.select(next_population_candidates)
self.score_history.append(self.global_score)
return geneartion
ABC Solver#
Solution class for Artificial Bee Colony Solver
class AritificalBeeColonySolver:
def __init__(self, population_size=20):
self.global_solution = None
self.global_score = float('-inf')
self.max_iterations = 1000
self.num_of_bees = population_size
self.food_sources = []
self.food_source_size = self.num_of_bees // 2
self.improvement_histories = []
self.problem = None
self.pairs = None
self.score_history = []
self.converge_history = []
self.terminate_threshold = float('-inf')
def reset(self):
population_size = self.num_of_bees
self.__init__(population_size)
def update_global(self, score, solution):
if score > self.global_score:
self.global_solution = solution
self.global_score = score
def move_around(self, source):
for i in range(10):
i, j = random.sample(range(len(source)), 2)
source[i], source[j] = source[j], source[i]
return source
def employ_bee_update(self, source_id):
source = self.food_sources[source_id]
neighbour = self.move_around(source)
diff = self.evaluate(neighbour) - self.problem.evaluate(source)
self.improvement_histories[source_id].append(diff > 0)
if diff > 0:
return neighbour
return source
def get_abandoned(self):
abandoned = []
for i, improvement_history in enumerate(self.improvement_histories):
if len(improvement_history) > 10:
if sum(improvement_history[-10:]) / 10 <= 0.4:
abandoned.append(i)
return abandoned
def scout_bee_update(self, source_id):
random.shuffle(self.food_sources[source_id])
self.evaluate(self.food_sources[source_id])
self.improvement_histories[source_id] = [True]
return self.food_sources[source_id]
def evaluate(self, solution):
score = self.problem.evaluate(solution)
self.update_global(score, solution)
return score
def solve(self, problem):
self.problem = problem
for _ in range(self.food_source_size):
food_source = problem.get_initial_soluton()
self.evaluate(food_source)
self.food_sources.append(food_source)
self.improvement_histories.append([True])
for iteration in tqdm(range(self.max_iterations)):
for i in range(self.num_of_bees // 2):
self.food_sources[i] = self.employ_bee_update(i)
for _ in range(self.num_of_bees // 2):
scores = [ self.evaluate(source) for source in self.food_sources ]
distribution = [ s / sum(scores) for s in scores ]
i = random.choices(range(0, self.food_source_size), k=1, weights=distribution)[0]
self.food_sources[i] = self.employ_bee_update(i)
self.converge_history.append(np.average(scores))
for i in self.get_abandoned():
self.food_sources[i] = self.scout_bee_update(i)
self.score_history.append(self.global_score)
if len(self.score_history) > 10:
if np.var(self.score_history[-10:]) < self.terminate_threshold:
break
return iteration
Solving the Problem#
We can solve the problem using different algorithms and compare the results.
For this case, we will assume the following parameters:
p = Problem(use_soft_constraint=True,alpha=1e-5, number_of_tour=2)
GA Solution#
This implementation seeks to produce two tours, using the Genetic Algorithm Solver.
# defaults are max_generations = 1000, population_size = 20
ga = GeneticAlgorithmSolver()
ga.solve(p)
sol = p.gaint_tour_decode([p.id_pois_map[i] for i in ga.global_solution])
Visualizing Results#
Problem.draw_tours(sol)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
/tmp/ipykernel_4124/3014936520.py in <module>
----> 1 Problem.draw_tours(sol)
/tmp/ipykernel_4124/703988465.py in draw_tours(tours)
128 if i == len(tour) - 1:
129 i = 0
--> 130 folium.Marker(location=loc, icon=folium.Icon(color='white', icon_color='white')).add_to(m)
131 folium.Marker(location=list(v.coordinates)[::-1], icon=number_DivIcon(color,i)).add_to(m)
132 r = u.route_to(v)['coords']
NameError: name 'loc' is not defined
data = ga.converge_history
plt.plot(list(range(len(data))),data)
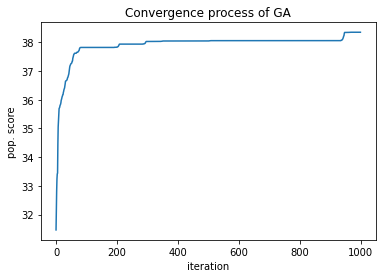
plt.title('Convergence process of GA')
plt.xlabel('iteration')
plt.ylabel('pop. score')
print('The final solution has a score of', str(ga.global_score))
The final solution has a score of 38.348292
Adaptive GA Solution#
# defaults are max_generations = 1000, population_size = 20
aga = AdaptiveGeneticAlgorithmSolver()
aga.solve(p)
sol = p.gaint_tour_decode([p.id_pois_map[i] for i in aga.global_solution])
100%|██████████| 1000/1000 [00:01<00:00, 511.04it/s]
Visualizing Results#
Problem.draw_tours(sol)
data = aga.converge_history
plt.plot(list(range(len(data))),data)
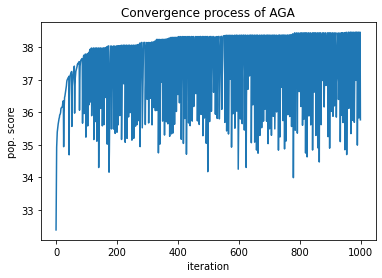
plt.title('Convergence process of AGA')
plt.xlabel('iteration')
plt.ylabel('pop. score')
print('The final solution has a score of', str(aga.global_score))
The final solution has a score of 38.455375000000004
ABC Solution#
abc = AritificalBeeColonySolver()
abc.solve(p)
sol = p.gaint_tour_decode([p.id_pois_map[i] for i in abc.global_solution])
100%|██████████| 1000/1000 [00:04<00:00, 216.50it/s]
Visualizing Results#
Problem.draw_tours(sol)
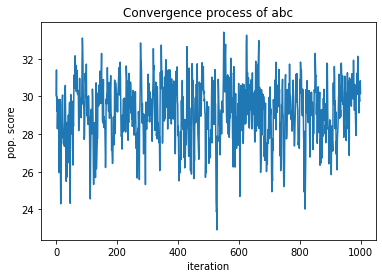
data = abc.converge_history
plt.plot(list(range(len(data))),data)
plt.title('Convergence process of abc')
plt.xlabel('iteration')
plt.ylabel('pop. score')
print('The final solution has a score of', str(abc.global_score))
The final solution has a score of 37.176791
Comparative Analysis#
We can also compare the results across the different approaches in terms of wall time, cpu time, score, and optimality.
This can be done by first storing the runtime results in experiment files, and plotting the results side by side.
class Experiment:
def __init__(self, problem, solver, num_run=5, cold=True, population_size=20):
if problem is None:
return
self.optimal_score = problem.number_of_tour * 5.0 * 4.0
self.start_cold = cold
self.solver = solver
self.problem = problem
self.num_run = num_run
self.population_size = population_size
self.result = {
"wall_time":[],
"cpu_time":[],
"score":[],
"optimality":[],
"num_iteration":[],
}
self.score_histories = []
def load_experiment_results(self, file_name):
with open(file_name) as f:
result = json.loads(f.read())
self.optimal_score = result["optimal_score"]
self.start_cold = result["start_cold"]
self.num_run = result["num_run"]
self.population_size = result["population_size"]
self.result = result["result"]
self.score_histories = result["score_histories"]
def store_experiment_results(self):
experiment_result = {
"optimal_score": self.optimal_score,
"start_cold": self.start_cold,
"solver": type(self.solver).__name__,
"soft_constraint": self.problem.use_soft_constraint,
"alpha": self.problem.alpha,
"number_of_tour": self.problem.number_of_tour,
"num_run": self.num_run,
"population_size": self.population_size,
"result": self.result,
"score_histories": self.score_histories
}
file_name = "experiment/{}_{}_{}_{}.json".format(experiment_result["solver"], experiment_result["number_of_tour"], experiment_result["population_size"], int(time.time()))
with open(file_name, 'w+') as f:
f.write(json.dumps(experiment_result))
def warm_up_cache(self):
for _ in range(5):
self.solver.solve(self.problem)
self.solver.reset()
def get_mean_result(self):
mean_result = {}
for key, value in self.result.items():
mean_result[key] = round (sum(value) / len(value), 3)
return mean_result
def get_max_result(self):
mean_result = {}
for key, value in self.result.items():
mean_result[key] = max(value)
return mean_result
def get_min_result(self):
mean_result = {}
for key, value in self.result.items():
mean_result[key] = min(value)
return mean_result
def get_mean_global_score_history(self):
mean_score = []
history_len = len(self.score_histories[0])
for i in range(history_len):
val = 0
for score_history in self.score_histories:
val += score_history[i]
val /= len(self.score_histories)
mean_score.append(val)
return mean_score
def plot_global_score_history(self):
for score_history in self.score_histories:
plt.plot(score_history)
plt.show()
def plot_mean_global_score_history(self):
mean_score = self.get_mean_global_score_history()
plt.plot(mean_score)
plt.show()
def get_num_iteration_to_pdbk(self, pdbk, score_history):
score_cut = self.optimal_score - pdbk * self.optimal_score
for i, score in enumerate(score_history):
if score >= score_cut:
return i
return None
def get_mean_num_iteration_to_pdbk(self, pdbk):
cut_points = []
for score_history in self.score_histories:
cut_point = self.get_num_iteration_to_pdbk(pdbk, score_history)
if cut_point is not None:
cut_points.append(cut_point)
else:
cut_points.append(10000)
return sum(cut_points) / len(cut_points)
def run(self):
if self.start_cold is False:
self.warm_up_cache()
for i in range(self.num_run):
wall_time_start = time.perf_counter()
cpu_time_start = time.process_time()
num_iteration = self.solver.solve(self.problem)
wall_time_end = time.perf_counter()
cpu_time_end = time.process_time()
self.result["wall_time"].append( wall_time_end - wall_time_start )
self.result["cpu_time"].append( cpu_time_end - cpu_time_start )
self.result["score"].append( self.solver.global_score )
self.result["optimality"].append( ( self.optimal_score - self.solver.global_score ) / self.optimal_score )
self.result["num_iteration"].append( num_iteration )
self.score_histories.append( self.solver.score_history )
self.solver.reset()
if self.start_cold is True:
self.problem.reset()
num_run = 3
cold = True
population_sizes = [20]
number_of_tours = [2]
for population_size in population_sizes:
for number_of_tour in number_of_tours:
experiment = Experiment(Problem(use_soft_constraint=True,alpha=1e-5,number_of_tour=number_of_tour),
GeneticAlgorithmSolver(population_size=population_size),
num_run=num_run, cold=cold, population_size=population_size)
experiment.run()
experiment.store_experiment_results()
experiment = Experiment(Problem(use_soft_constraint=True,alpha=1e-5,number_of_tour=number_of_tour),
AdaptiveGeneticAlgorithmSolver(population_size=population_size),
num_run=num_run, cold=cold, population_size=population_size)
experiment.run()
experiment.store_experiment_results()
experiment = Experiment(Problem(use_soft_constraint=True,alpha=1e-5,number_of_tour=number_of_tour),
AritificalBeeColonySolver(population_size=population_size),
num_run=num_run, cold=cold, population_size=population_size)
experiment.run()
experiment.store_experiment_results()
100%|██████████| 1000/1000 [00:01<00:00, 896.31it/s]
100%|██████████| 1000/1000 [00:00<00:00, 2080.58it/s]
100%|██████████| 1000/1000 [00:00<00:00, 1967.19it/s]
100%|██████████| 1000/1000 [00:02<00:00, 467.82it/s]
100%|██████████| 1000/1000 [00:01<00:00, 503.97it/s]
100%|██████████| 1000/1000 [00:02<00:00, 468.37it/s]
100%|██████████| 1000/1000 [00:04<00:00, 214.88it/s]
100%|██████████| 1000/1000 [00:04<00:00, 217.94it/s]
100%|██████████| 1000/1000 [00:04<00:00, 217.11it/s]
Visualizing Results#
from glob import glob
import os
mean_scores = []
labels = []
for path_name in glob("experiment/*"):
file_name = os.path.basename(path_name).split('.')[0]
solver, num_tour, population, _ = file_name.split('_')
experiment = Experiment(None, None)
experiment.load_experiment_results(path_name)
mean_scores.append(experiment.get_mean_global_score_history())
labels.append("{}-{}".format(solver[:-6], population))
print("{}-{}".format(solver[:-6], population), "average result:", experiment.get_mean_result())
plt.figure(figsize=(16, 12))
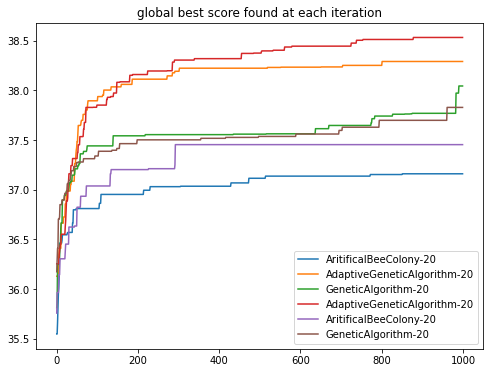
plt.title("Global Best Score found at each Iteration")
for label, mean_score in zip(labels, mean_scores):
plt.plot(mean_score, label=label)
_ = plt.legend()
AritificalBeeColony-20 average result: {'wall_time': 4.619, 'cpu_time': 4.629, 'score': 37.16, 'optimality': 0.071, 'num_iteration': 999.0}
AdaptiveGeneticAlgorithm-20 average result: {'wall_time': 12.456, 'cpu_time': 12.344, 'score': 38.291, 'optimality': 0.043, 'num_iteration': 999.0}
GeneticAlgorithm-20 average result: {'wall_time': 0.707, 'cpu_time': 0.709, 'score': 38.044, 'optimality': 0.049, 'num_iteration': 999.0}
AdaptiveGeneticAlgorithm-20 average result: {'wall_time': 2.091, 'cpu_time': 2.096, 'score': 38.533, 'optimality': 0.037, 'num_iteration': 999.0}
AritificalBeeColony-20 average result: {'wall_time': 28.616, 'cpu_time': 28.161, 'score': 37.454, 'optimality': 0.064, 'num_iteration': 999.0}
GeneticAlgorithm-20 average result: {'wall_time': 4.132, 'cpu_time': 4.099, 'score': 37.829, 'optimality': 0.054, 'num_iteration': 999.0}