Particle Swarm Optimization

Particle Swarm Optimization (PSO) works by generating a number of candidates (or particles) and moving those candidates along the search space in search of the optimal solution. Each particle moves according to some predefined rules, which are influenced by the currently known best position, as well as the universally known best position.

Essentially, each particle takes into account the following:

1. Predetermined rules for movement.

2. What the particle knows about the best direction to move.

3. What the system as a whole knows about the best direction to move.

This mechanism allows the collective whole to “swarm” or congregate towards good solutions, and replicates the behaviours of natural swarms and flocks, such as those seen in birds, fish, or bees.

Example implementation

We can design a simple implementation of PSO to showcase its features.

Consider a function as follows:

\(f(x)=0.2\sqrt{(x-1)^2}+100(\cos(x)+\sin(x))\)

Our goal is to minimize the collective sum (or cost), given a population of size \(n\).

import numpy as np
from tqdm.notebook import tqdm

# The function
fn = lambda x: (0.2*np.sqrt((x-1)**2)+100*(np.cos(x)+np.sin(x)))
fn = np.vectorize(fn)

# Initialize parameters
n = 100 # population size
npar = 20 # number of dimensions
maxit = 10 # number of iterations
c1 = 1 # cognitive parameter
c2 = 4-c1 # social parameter

par = np.random.rand(n, npar)
vel = np.random.rand(n, npar)
cost = fn(par) # the global cost as a numpy array

global_best = np.amin(par, axis=0)
localpar = par
localcost = cost
current_mean = par.mean()
states = []

for itr in tqdm(range(maxit)):
    w = (maxit - itr) / maxit
    r1 = np.random.rand(n, npar)
    r2 = np.random.rand(n, npar)
    vel = (
        w * vel
        + c1 * r1 * (localpar - par)
        + c2 * r2 * (np.ones((n, 1)) * global_best - par)
    )
    par = par + vel
    overlimit = par <= 1
    underlimit = par >= 0
    par = par * overlimit + (overlimit ^ True)
    par = par * underlimit
    cost = fn(par)
    temp = np.amin(par, axis=0)
    if temp.sum() < global_best.sum():
        global_best = temp
    if par.sum() < localpar.sum():
        localpar = par
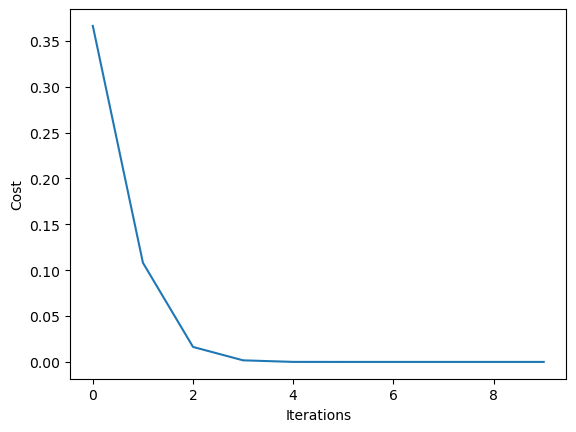
    states.append(par.mean())

import matplotlib.pyplot as plt
plt.plot(states)
plt.ylabel('Cost')
plt.xlabel('Iterations')
plt.show()

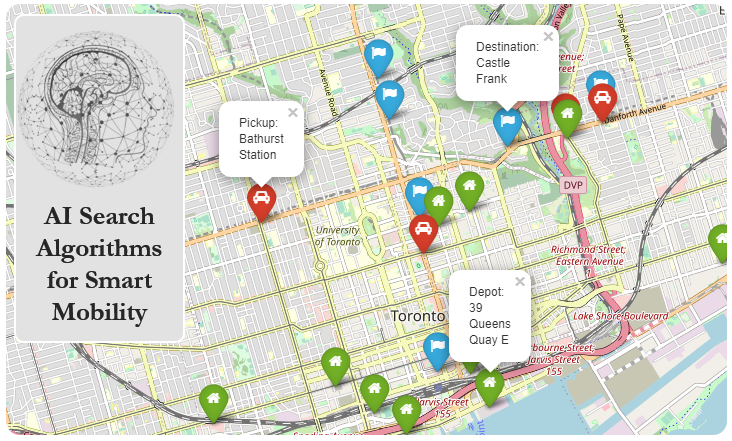
Example: PSO with Routing Problem

import osmnx
from smart_mobility_utilities.common import Node, cost, randomized_search
from smart_mobility_utilities.viz import draw_route
from smart_mobility_utilities.problem import cross_over
import random
import itertools
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt

reference = (43.661667, -79.395)

G = osmnx.graph_from_point(reference, dist=300, clean_periphery=True, simplify=True)

origin = Node(graph=G, osmid=55808290)
destination = Node(graph=G, osmid=389677909)

highlighted = [389677909, 55808290]

# marking both the source and destination node

nc = ['red' if node in highlighted else '#336699' for node in G.nodes()]
ns = [50 if node in highlighted else 8 for node in G.nodes()]
fig, ax = osmnx.plot_graph(G, node_size=ns, node_color=nc, node_zorder=2)

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [5], in <cell line: 2>()
      1 import osmnx
----> 2 from smart_mobility_utilities.common import Node, cost, randomized_search
      3 from smart_mobility_utilities.viz import draw_route
      4 from smart_mobility_utilities.problem import cross_over

ModuleNotFoundError: No module named 'smart_mobility_utilities'

# Initialize the swarm
n = 200
particles = [randomized_search(G,origin.osmid, destination.osmid) for _ in range(n)]
num_swarms = 4
num_iterations = 100

# Used to track the costs for analysis
swarm_costs = []

for iteration in tqdm(range(num_iterations)):
    particles.sort(key=lambda p: cost(G,p))
    pps = n // num_swarms # particles per swarm

    # We select the best particles in each swarm to lead
    leaders = particles[:pps][:]

    for i in range(num_swarms):
        particles[i] , particles[i * (pps) - 1] = particles[i * (pps) - 1], particles[i]
    
    swarms = list()
    for i in range(num_swarms):
        swarms.append(particles[i * (pps): i*(pps) + pps])

    # For each swam, we need to follow the leader of that swarm

    # follow the leader of the local swarm
    def local_follow(population):
        for i in range(1, len(population)):
            population[i] = cross_over(population[0],population[i])

    # follow the global leader
    def global_follow():
        for u, v in itertools.product(range(0, len(leaders)), range(0, len(leaders))):
            to_be_mutated = random.choice([u, v])
            leaders[to_be_mutated] = cross_over(leaders[u], leaders[v])
    
    for swarm in swarms:
        local_follow(swarm)
    
    global_follow()

    # Add the new leaders
    particles[i*(pps-1)] = leaders[i]

    # Track the lowest cost in each swarm
    swarms = list()
    for i in range(num_swarms):
        swarms.append(particles[i * (pps): i*(pps) + pps])

    cost_set = []
    for swarm in swarms:
        lowest =min([cost(G,p) for p in swarm])
        cost_set.append(lowest)
    swarm_costs.append(cost_set)

route = min(particles, key=lambda p: cost(G,p))
print("Cost:",cost(G,route))
draw_route(G, route)

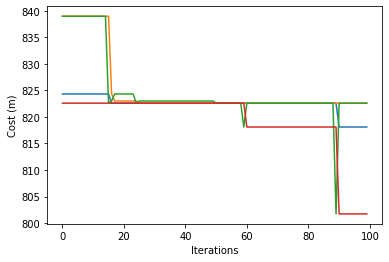
Cost: 801.235

plt.plot(swarm_costs)
plt.xlabel('Iterations')
plt.ylabel('Cost (m)')
plt.show()