Deadheading in Ride-Hailing#
Authors: Juan Carrillo, Anas Mahmoud and Sheran Cardoza
Course: ECE1724H: Bio-inspired Algorithms for Smart Mobility - Fall 2021
Instructor: Dr. Alaa Khamis
Department: Edward S. Rogers Sr. Department of Electrical & Computer Engineering, University of Toronto
Introduction#
Ridesharing is one of several on-demand mobility services gaining momentum in recent years and represents a flexible and convenient alternative for transportation. Despite its attractiveness, ridesharing also causes undesired effects such as increased traffic and emissions. In this project, we study specifically the problem of ridesharing vehicles roaming without passengers, also known as deadheading.
import copy
import time
import random
import statistics
from math import cos
from configparser import ConfigParser
# Data and plotting
import numpy as np
import pandas as pd
from pandas.io import parsers
import folium
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
# Mobility
import osmnx
from smart_mobility_utilities.common import Node
from smart_mobility_utilities.common import cost
from smart_mobility_utilities.viz import draw_route
from smart_mobility_utilities.search import dijkstra, astar
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Input In [1], in <cell line: 18>()
16 # Mobility
17 import osmnx
---> 18 from smart_mobility_utilities.common import Node
19 from smart_mobility_utilities.common import cost
20 from smart_mobility_utilities.viz import draw_route
ModuleNotFoundError: No module named 'smart_mobility_utilities'
Data#
The data source for this example contains 175 delivery records for addresses in the Greater Toronto Area (GTA).
These entries with latitude and longitude information are then converted into OSM Node IDs (closest node). One location is assigned per vehicle as a “initial depot location”. Each rider is assigned a pickup node and a dropoff node.
Problem Classes#
Rider#
class Rider(object):
def __init__(
self,
id: int,
pickup_location: tuple,
dropoff_location: tuple,
pickup_map_node_id: int,
dropoff_map_node_id: int
):
""" Instantiate a rider object
Parameters
----------
id : A unique id for each rider
pickup_location: pickup lat and long
dropoff_location: dropoff lat and long
pickup_map_node_id: osmid of the nearest node to pickup_location
dropoff_map_node_id: osmid of the nearest node to dropoff_location
"""
self.id = id
self.pickup_location = pickup_location
self.dropoff_location = dropoff_location
self.pickup_map_node_id = pickup_map_node_id
self.dropoff_map_node_id = dropoff_map_node_id
def __str__(self)->str:
return "ID of rider: {}\n".format(self.id) + \
"Pickup location of rider: {} {}\n".format(self.pickup_location[0], self.pickup_location[1]) + \
"Dropoff location of rider: {} {}\n".format(self.dropoff_location[0], self.dropoff_location[1]) + \
"Pickup node id of rider: {}\n".format(self.pickup_map_node_id) + \
"Dropoff node id of rider: {}\n".format(self.dropoff_map_node_id)
Driver#
class Driver(object):
def __init__(
self,
id,
initial_location: tuple,
initial_map_node_id: int
):
"""Instantiate a drive object
Parameters
----------
id : A unique id for each driver
initial_location: initial lat and long
initial_map_node_id: osmid of the nearest node to initial driver location
"""
self.id = id
self.initial_location = initial_location
self.initial_map_node_id = initial_map_node_id
def __str__(self) -> str:
return "ID of driver: {}\n".format(self.id) + \
"Initial location of driver: {} {}\n".format(self.initial_location[0], self.initial_location[1]) + \
"Initial node id of driver: {}\n".format(self.initial_map_node_id)
Coord (Node)#
class Coord(object):
def __init__(self, lat, lng, osmid):
self.lat = lat
self.lng = lng
self.osmid = osmid
def __repr__(self):
return "[lat,lng,id]=[{},{},{}]".format(self.lat, self.lng, self.osmid)
def __eq__(self, other):
if isinstance(other, Coord):
return self.osmid == other.osmid
return False
def __ne__(self, other):
return not self == other
Data Sampler#
This class processes raw data and converts into a usable format.
class Sampler(object):
def __init__(self):
pass
def prepare_data(self, df):
"""Convert raw data to custom data format
Parameters
----------
df : dataframe object of raw data
Returns
----------
dataframe object of custom data
"""
df = df.drop_duplicates()
# Pick midpoint of all coordinates as the center of the graph
self.midpoint = (df['dropoff_lat'].mean(), df['dropoff_lng'].mean())
# Calculate radius as distance of farthest coordinate from midpoint
dists = [osmnx.distance.great_circle_vec(self.midpoint[0], self.midpoint[1], row['dropoff_lat'], row['dropoff_lng']) for _, row in df.iterrows()]
self.radius = max(dists)
# self.radius = 2000
# Generate graph (takes a long time)
graph = osmnx.graph.graph_from_point(
self.midpoint, dist=self.radius, clean_periphery=True, simplify=True)
# Project graph
#graph = osmnx.project_graph(graph, to_crs={'init': 'epsg:32617'})
# Extract coord info
lats = []
lngs = []
osmids = []
for index, row in df.iterrows():
lat = row['dropoff_lat']
lng = row['dropoff_lng']
osmid = osmnx.distance.nearest_nodes(graph, lng, lat)
lats.append(lat)
lngs.append(lat)
osmids.append(osmid)
# Create dataframe
new_df = pd.DataFrame(list(zip(lats, lngs, osmids)),
columns=['lat','lng','osmid'])
def init_data(self, df):
"""Initialize Sampler class attributes with prepared data
Parameters
----------
df : dataframe object of prepared data
"""
df = df.drop_duplicates()
# Pick midpoint of all coordinates as the center of the graph
self.midpoint = (df['lat'].mean(), df['lng'].mean())
# Calculate radius as distance of farthest coordinate from midpoint
dists = [osmnx.distance.great_circle_vec(self.midpoint[0], self.midpoint[1], row['lat'], row['lng']) for _, row in df.iterrows()]
self.radius = max(dists)
# Extract coords
self.coords = [Coord(row['lat'], row['lng'], row['osmid']) for _,row in df.iterrows()]
# Debug info
print("Num coords = {}".format(len(self.coords)))
seen = set()
unique_ids = [seen.add(coord.osmid) or coord for coord in self.coords if coord.osmid not in seen]
print("Num coords with unique node id = {}".format(len(unique_ids)))
def get_samples(self, n_drivers, n_riders, radius=None, midpoint=None, return_graph=True):
"""Return sample data containing drivers, riders, and graph
Parameters
----------
n_drivers : number of drivers
n_riders : number of riders
radius : radius in metres
midpoint : midpoint as a tuple of (lat, lng)
return_graph: generate a graph based on midpoint and radius
Returns
---------
drivers : list of Driver objects
riders : list of Rider objects
graph : (optional) if return_graph=True, returns graph of nodes
"""
assert n_drivers < n_riders
midpoint = self.midpoint if midpoint is None else midpoint
radius = self.radius if radius is None else radius
# Find valid coords within this radius
coords = []
for coord in self.coords:
dist = osmnx.distance.great_circle_vec(midpoint[0], midpoint[1], coord.lat, coord.lng)
if dist <= radius:
coords.append(coord)
assert n_drivers + n_riders * \
2 <= len(coords), "Error: n_drivers={} + n_riders*2={} > available_coords={}".format(
n_drivers, n_riders*2, len(coords))
# Shuffle the coords for some randomization
# commented for debugging purposes
random.shuffle(coords)
# Assign drivers
drivers = []
for i, coord in enumerate(coords):
if i < n_drivers:
drivers.append(Driver(i, (coord.lat, coord.lng), coord.osmid))
else:
# Delete the drivers
coords = coords[i+1:]
break
# Delete any excess coords we don't need
coords = coords[0:2*n_riders]
# Assign riders
riders = []
it = iter(coords)
for i, coord in enumerate(it):
pickup = coord
dropoff = next(it)
riders.append(Rider(i, (pickup.lat, pickup.lng),
(dropoff.lat, dropoff.lng), pickup.osmid, dropoff.osmid))
if return_graph:
# Generate graph for this custom radius
graph = osmnx.graph.graph_from_point(
midpoint, dist=radius, clean_periphery=True, simplify=True)
return drivers, riders, graph
return drivers, riders
sampler = Sampler()
# Data preparation takes a long time.
# Run just once and save to a CSV, then in subsequent runs
# just use the saved CSV.
# Load in the data
start = time.time()
filename = 'PreparedData.csv'
df = pd.read_csv(filename)
sampler.init_data(df)
end = time.time()
print("Data init time = {} seconds".format(end - start))
Num coords = 169
Num coords with unique node id = 168
Data init time = 0.016378164291381836 seconds
start = time.time()
radius = 6000
num_drivers = 3
num_riders = 7
dt_midpoint = (43.653225, -79.383186)
drivers, riders, graph = sampler.get_samples(
num_drivers, num_riders, radius=radius, midpoint=dt_midpoint, return_graph=True)
end = time.time()
print("Samples time = {} seconds".format(end - start))
print("Samples contains the following:")
print(f'{len(drivers)} drivers')
print(f'{len(riders)} riders')
print(f'{len(graph.nodes())} graph nodes')
Samples time = 25.41386079788208 seconds
Samples contains the following:
3 drivers
7 riders
48273 graph nodes
Plot#
Used to visualize coordinates on a map.
class Plot():
def __init__(self, drivers, riders, graph) -> None:
"""Initializes a plot object
Args:
drivers (list): drivers available
riders (list): riders requesting service
graph (networkx.classes.multidigraph.MultiDiGraph): road network
"""
self.drivers = drivers
self.riders = riders
self.graph = graph
self.map = None
def calc_centroid(self):
""" calculates centroid of points to plot
Returns:
list: latitude and longitude values of the centroid
"""
avg_lat = 0
avg_lon = 0
total_coords = len(self.drivers) + 2*len(self.riders)
for driver in self.drivers:
driver_ini_lat, driver_ini_lon = driver.initial_location
avg_lat += driver_ini_lat
avg_lon += driver_ini_lon
for rider in self.riders:
rider_pic_lat, rider_pic_lon = rider.pickup_location
rider_dro_lat, rider_dro_lon = rider.dropoff_location
avg_lat += rider_pic_lat + rider_dro_lat
avg_lon += rider_pic_lon + rider_dro_lon
avg_lat /= total_coords
avg_lon /= total_coords
return [avg_lat, avg_lon]
def init_basemap(self):
""" initializes a folium basemap centered over drivers and riders
"""
self.map = folium.Map(location=self.calc_centroid(), zoom_start=10)
def add_pins_to_basemap(self):
""" adds locations to basemap
"""
# checks that a basemap is initialized
assert (self.map is not None), "must initialize basemap before adding locations"
for driver in self.drivers:
folium.Marker(location=list(driver.initial_location),
popup=f'driver {driver.id}',
icon=folium.map.Icon(color='orange')
).add_to(self.map)
for rider in self.riders:
folium.Marker(location=list(rider.pickup_location),
popup=f'rider {rider.id}: pickup',
icon=folium.map.Icon(color='blue')
).add_to(self.map)
folium.Marker(location=list(rider.dropoff_location),
popup=f'rider {rider.id}: dropoff',
icon=folium.map.Icon(color='red')
).add_to(self.map)
def basemap_to_html(self):
""" exports the basemap with pins to html
"""
# checks that a basemap is initialized
assert (self.map is not None), "must initialize basemap before saving"
self.map.save('basemap_with_pins.html')
def plot_graph_with_nodes(self):
""" plots the graph with nodes classified in colors
Args:
graph
"""
colors_dict = self.get_colors_dict()
all_nodes_colors = self.get_nodes_colors(colors_dict)
all_nodes_size = [50 if node_id in colors_dict.keys() else 2
for node_id in self.graph.nodes]
fig, ax = osmnx.plot_graph(
self.graph, node_size=all_nodes_size,
node_color=all_nodes_colors, node_zorder=2,
bgcolor='#F2F3F5', edge_color='#B3B5B7',
save=True, filepath='graph_and_nodes.png')
def get_colors_dict(self):
""" generates a dictionary mapping node ids to colors
Returns:
colors_dict
"""
c_orange = '#FF8A33' # drivers
c_blue = '#3AACE5' # rider pickup
c_red = '#FF3352' # rider drop off
colors_dict = {}
for driver in self.drivers:
colors_dict[driver.initial_map_node_id] = c_orange
for rider in self.riders:
colors_dict[rider.pickup_map_node_id] = c_blue
colors_dict[rider.dropoff_map_node_id] = c_red
return colors_dict
def get_nodes_colors(self, colors_dict):
""" generates a list with color for each node id in graph
Args:
colors_dict
Returns:
all_nodes_colors
"""
c_grey = '#B3B5B7'
all_nodes_colors = []
for node_id in self.graph.nodes:
try:
all_nodes_colors.append(colors_dict[node_id])
except:
all_nodes_colors.append(c_grey)
return all_nodes_colors
Problem Formulation#
Formulation#
The evaluation function is a multi-objective cost function and includes:
Minimizing deadheading by searching for solutions that reduce miles driven without passengers,
Maximizing fairness between independent drivers by encouraging solutions that minimize the standard deviation of the ratio between miles driven with a passenger over miles driven without a passenger
Maximizing fairness between wait-time of customers by minimizing the standard deviation of customer’s wait time
Maximizing profit by serving higher priority customers before lower priority customers.
The following is the multi-objective function that we wish to minimize:
Subject to:
The first constraint shown in eq.2, ensures that the weights of each objective sums up to one. In eq.3 we ensure that every customer is assigned to only one driver and therefore also guarantees that all customers are matched, while in eq.4, we ensure that all customers are matched only once (i.e., no customer is matched to the same driver twice). Finally, the last constraint shown in eq.5 ensures that the wait time for any customer has to be less than or equal \(T_{max}\) otherwise the solution would not be feasible.
The design variable in this problem is the list of lists defining the order of assignments of customers to drivers and is denoted by \(D\).
Variables:
\(C\): List of customers to be served.
\(c_i\): A unique ID assigned each customer
\(c_{i, cl}\): 2D collection point of the \(i^{th}\) customer.
\(c_{i, dr}\): 2D drop-off point of the \(i^{th}\) customer.
\(t(i, j)\): Drive time of the shortest path between node \(i\) and \(j\).
\(dis(i, j)\): Distance of the shortest path between node \(i\) and \(j\).
\(d_{j, 0}\): Node representing the initial 2D location of \(j^{th}\) driver.
\(D\): List of assignments for participating drivers. Each element of the list is a list of customers assigned to a driver.
\(d_j\): Ordered list of customers assigned to \(j_{th}\) driver. Order defines the sequence of service.
\(Pr_j\): Total profitable miles driven by \(j^{th}\) driver.
\(Dh_j\): Total deadheading miles driven by \(j^{th}\) driver.
\(\mu_{pd}\): Mean ratio between \(Pr_j\) and \(Dh_j\) of all drivers for a given solution.
\(ds_i\): Distance travelled before serving \(i^{th}\) customer.
\(ts_i\): Time taken before serving \(i^{th}\) customer.
\(\mu_{{ds}}\): Mean of distance travelled before serving any customer for a given solution.
\(T_{max}\): Maximum wait time for any customer.
Solution Class#
class DeadHeadingProblemEvaluation:
"""Evaluate feasiblity and Cost of a solution to the Deadheading Problem.
"""
def __init__(
self,
graph,
drivers,
riders,
alpha_deadheading=0.8,
alpha_driver_fairness=0.1,
alpha_rider_fairness=0.1
):
"""Initialize with problem parameters and do some precomputation.
Parameters
----------
graph: map consists of nodes (used to compute shortest path)
drivers : A list of driver objects
riders : A list of rider objects
"""
self.graph = graph
self.drivers = list(drivers)
self.riders = list(riders)
# weights for cost function
self.alpha_deadheading = alpha_deadheading
self.alpha_driver_fairness = alpha_driver_fairness
self.alpha_rider_fairness = alpha_rider_fairness
assert self.alpha_deadheading + self.alpha_driver_fairness + self.alpha_rider_fairness == 1
# Generate dist_matrix that is indexed by (from_osmid, to_osmid) and returns distance
self.dist_matrix = {}
def add_dist(from_id, to_id):
from_node = Node(graph=graph, osmid=from_id)
to_node = Node(graph=graph, osmid=to_id)
shortest_route = astar(
G=graph, origin=from_node, destination=to_node)
cost_route = cost(graph, shortest_route)
self.dist_matrix[(from_id, to_id)] = cost_route
# driver initial -> rider pickup
for driver in drivers:
for rider in riders:
add_dist(driver.initial_map_node_id, rider.pickup_map_node_id)
# rider dropoff -> rider pickup
for rider1 in riders:
for rider2 in riders:
if rider1 is not rider2:
add_dist(rider1.dropoff_map_node_id,
rider2.pickup_map_node_id)
# rider pickup -> dropoff
for rider in riders:
add_dist(rider.pickup_map_node_id, rider.dropoff_map_node_id)
def set_solution(self, solution):
"""Add solution to evaluate, and do some precomputation.
Parameters
----------
solution: A list of lists
"""
self.solution = solution
# constraints
assert len(self.solution) == len(self.drivers)
self.unique_assignment_constraint()
self.match_all_riders_constraint()
# compute distances once to speed up evaluation
self.deadheading_miles, self.profitable_mile, self.prearrival_miles = self.get_driver_deadhead_profit()
def evaluate_cost_func(self):
return self.alpha_deadheading * self.evaluate_deadheading_cost() + \
self.alpha_driver_fairness * self.evaluate_driver_fairness() + \
self.alpha_rider_fairness * self.evaluate_rider_fairness()
def evaluate_deadheading_cost(self):
return sum(self.deadheading_miles)
def evaluate_driver_fairness(self):
delta_pr_dh = [abs(pr-dh) for dh,
pr in zip(self.deadheading_miles, self.profitable_mile)]
return statistics.stdev(delta_pr_dh)
def evaluate_rider_fairness(self):
# Flatten prearrival times into a 1D list
all_prearrival_miles = sum(self.prearrival_miles, [])
return statistics.stdev(all_prearrival_miles)
# return deadhing miles and profitable miles for each driver
def get_driver_deadhead_profit(self):
deadheading_miles = [] # deadheading miles for each driver
profitable_miles = [] # profitable miles for each driver
prearrival_miles = [] # same format as solution, represents driver miles travelled before reaching this rider
# loop over drivers
for driver_idx, riders in enumerate(self.solution):
driver = self.drivers[driver_idx]
dh_miles = 0
pr_miles = 0
pa_miles = []
# loop over riders of current driver
for rider_idx, rider in enumerate(riders):
# deadheading
if rider_idx == 0:
dh_miles += self.dist(osmid_a=driver.initial_map_node_id,
osmid_b=rider.pickup_map_node_id)
else:
prev_rider = riders[rider_idx-1]
dh_miles += self.dist(osmid_a=prev_rider.dropoff_map_node_id,
osmid_b=rider.pickup_map_node_id)
# prearrival
pa_miles.append(pr_miles + dh_miles)
# profit
pr_miles += self.dist(osmid_a=rider.pickup_map_node_id,
osmid_b=rider.dropoff_map_node_id)
# populate total deadhing and profitable miles for current driver
deadheading_miles.append(dh_miles)
profitable_miles.append(pr_miles)
prearrival_miles.append(pa_miles)
return deadheading_miles, profitable_miles, prearrival_miles
def unique_assignment_constraint(self):
# loop over riders
for rider in self.riders:
# loop over assiment list of each driver
num_of_assignments = 0
for driver_solution in self.solution:
current_ids = [rider.id for rider in driver_solution]
if rider.id in current_ids:
num_of_assignments += 1
assert num_of_assignments == 1, "Error: Number of assignments for Rider: {} is {}, Expected assignment \
is 1".format(rider.id, num_of_assignments)
def match_all_riders_constraint(self):
number_of_assignments = sum(
[len(driver_assigment) for driver_assigment in self.solution])
assert number_of_assignments == len(
self.riders), "Number of assigned riders greater than number of riders!"
# Compute shortest path between two nodes on a graph
def dist(self, osmid_a: int, osmid_b: int):
return self.dist_matrix[(osmid_a, osmid_b)]
start = time.time()
eval_obj = DeadHeadingProblemEvaluation(graph, drivers, riders)
end = time.time()
print("Eval init time = {} seconds".format(end - start))
Eval init time = 12.58279013633728 seconds
Solution 1: Simulated Annealing#
class RandomSolution():
def __init__(self, drivers, riders):
self.drivers = drivers
self.riders = riders
# setting random seed from config file
config = ConfigParser()
config.read('config.ini')
#random.seed(config.get('main', 'seed'))
def get_random_sol(self):
# init random solution
rs = []
# add empty list for each driver
for i in range(len(self.drivers)):
rs.append([])
# add each rider to one driver
for rider in self.riders:
# random index within drivers list
r_idx = random.sample(range(len(self.drivers)), 1)[0]
rs[r_idx].append(rider)
return rs
class NeighborSolutions():
def __init__(self) -> None:
self.s = None
def set_solution(self, s):
self.s = s
def get_neigbors(self):
assert (self.s is not None), 'Must set solution first'
# driver swap
ds_sol = self.driver_swap(copy.deepcopy(self.s))
# rider reassign
rr_sol = self.rider_reassign(copy.deepcopy(self.s))
# rider shuffle
rs_sol = self.rider_shuffle(copy.deepcopy(self.s))
return [ds_sol, rr_sol, rs_sol]
def get_or_sol(self):
""" gets original variable """
return self.or_sol
def get_ds_sol(self):
""" gets driver swap """
return self.ds_sol
def get_rr_sol(self):
""" gets rider reassign """
return self.rr_sol
def get_rs_sol(self):
""" gets rider shuffle """
return self.rs_sol
def driver_swap(self, s):
""" swaps all riders between two drivers
Args:
s (list): original solution
Returns:
list: new solution
"""
num_drivers = len(s)
idx_swap = random.sample(range(num_drivers), 2)
temp_data = s[idx_swap[0]]
s[idx_swap[0]] = s[idx_swap[1]]
s[idx_swap[1]] = temp_data
return s
def rider_reassign(self, s):
""" reassigns one rider to another driver]
Args:
s (list): original solution
Returns:
list: new solution
"""
num_drivers = len(s)
while True:
# a driver giving one rider
d_giving = random.sample(range(num_drivers), 1)[0]
# checks the giving driver has at least one rider
if len(s[d_giving]) > 0:
break
r_available = len(s[d_giving]) # available number of riders
# index of moving rider
idx_moving = random.sample(range(r_available), 1)[0]
r_moving = s[d_giving].pop(idx_moving) # rider moving
while True:
d_receiving = random.sample(range(num_drivers), 1)[0]
# checks receiving driver is not giving driver
if d_giving != d_receiving:
c_riders = len(s[d_receiving])
if c_riders > 0:
idx_moving = random.sample(range(c_riders), 1)[0]
s[d_receiving].insert(idx_moving, r_moving)
else:
s[d_receiving].append(r_moving)
break
return s
def rider_shuffle(self, s):
""" shuffles riders of one driver
Args:
s (list): original solution
Returns:
list: new solution
"""
num_drivers = len(s)
while True:
# driver shuffling its riders
d_shuffling = random.sample(range(num_drivers), 1)[0]
if len(s[d_shuffling]) > 1:
random.shuffle(s[d_shuffling])
break
return s
def get_SA_parameters(drivers, riders, eval_obj, iterations, adaptive):
""" function that determines proper parameters for the SA method
Args:
drivers ([type]): [description]
riders ([type]): [description]
eval_obj ([type]): [description]
iterations ([type]): [description]
Returns:
[type]: [description]
"""
# number of random samples to get statistics from
num_samples = 100
# store cost of sample solutions
sample_sol_c = []
for i in range(num_samples):
# random solution
s = copy.deepcopy(RandomSolution(
drivers, riders).get_random_sol())
eval_obj.set_solution(s)
# cost of random solution
c = eval_obj.evaluate_cost_func()
sample_sol_c.append(c)
# average and standard deviation of cost
avg_c = np.array(sample_sol_c).mean()
std_c = np.array(sample_sol_c).std()
# setting initial temperature as
# 3.5 or 1.0 of the std of the cost of 100 random solutions
if adaptive:
k = 3.5 * std_c # encourage more exploration in adaptive version
else:
k = 1.5 * std_c
# final temperature is set to 0.1 std of cost
t_final = 0.1 * std_c
# extracting lambda from temperature equation
lam = -1 * (np.log(t_final/k)) / iterations
return (k, lam)
def runSA(drivers, riders, graph, eval_obj, k, lam, iterations, adaptive):
hist_solutions = []
hist_costs = []
sa_solver = SAnnealingSolver(
drivers, riders, graph, eval_obj, k, lam, adaptive)
solution_i, cost_i = sa_solver.get_status()
hist_solutions.append(solution_i)
hist_costs.append(cost_i)
for i in tqdm(range(iterations)):
sa_solver.obtain_neighbors()
sa_solver.pick_solution()
sa_solver.determine_next_solution()
solution_i, cost_i = sa_solver.get_status()
hist_solutions.append(solution_i)
hist_costs.append(cost_i)
return hist_solutions, hist_costs
def print_SA_states(states):
for i, value in enumerate(states):
print('--------------------------------------------')
print(f'Solution {i} cost -> {value[1]}')
def print_best(hist_costs):
best = np.array(hist_costs).min()
print('--------------------------------------------')
print('--------------------------------------------')
print(f'Best solution cost -> {best}')
print('--------------------------------------------')
print('--------------------------------------------')
Solver Class#
class SAnnealingSolver():
def __init__(self, drivers, riders, graph, eval_obj, k, lam, adaptive=False) -> None:
# problem setup
self.drivers = drivers
self.riders = riders
self.graph = graph
self.iteration = 0
# parameters of temperature schedule
self.schedule = self.exp_schedule(k, lam)
# simulated annealing variables
self.current_s = copy.deepcopy(RandomSolution(
drivers, riders).get_random_sol())
self.next_s = []
self.eval_obj = eval_obj
self.cost_current_s = self.get_cost(self.current_s)
self.neighbors = []
self.ns_generator = NeighborSolutions()
self.adaptive = adaptive
self.best_seen = copy.deepcopy(self.current_s)
# from https://smartmobilityalgorithms.github.io/book/content/TrajectoryAlgorithms/SimulatedAnnealing.html
def exp_schedule(self, k, lam):
# i corresponds to the iteration
def function(i): return (k * np.exp(-lam*i))
return function
def obtain_neighbors(self):
self.ns_generator.set_solution(copy.deepcopy(self.current_s))
self.neighbors = copy.deepcopy(self.ns_generator.get_neigbors())
def pick_solution(self):
# ------- adaptive part -------
if self.adaptive:
if self.get_cost(self.current_s) < self.get_cost(self.best_seen):
self.best_seen = self.current_s
candidate_from_neighbors = copy.deepcopy(
random.choice(self.neighbors))
self.next_s = copy.deepcopy(random.choice(
[candidate_from_neighbors, self.best_seen]))
else:
self.next_s = copy.deepcopy(random.choice(self.neighbors))
def get_cost(self, s):
self.eval_obj.set_solution(s)
return self.eval_obj.evaluate_cost_func()
def get_T(self, iteration):
return self.schedule(iteration)
# from https://github.com/SmartMobilityAlgorithms/smart_mobility_utilities/blob/master/smart_mobility_utilities/common.py
def probability(self, p):
return p > random.uniform(0.0, 1.0)
# from https://smartmobilityalgorithms.github.io/book/content/TrajectoryAlgorithms/SimulatedAnnealing.html
def determine_next_solution(self):
self.cost_current_s = self.get_cost(self.current_s)
cost_next_s = self.get_cost(self.next_s)
delta_e = cost_next_s - self.cost_current_s
self.iteration += 1
T = self.get_T(self.iteration)
if delta_e < 0 or self.probability(np.exp(-1 * delta_e/T)):
#coin = random.choice([1, 1, 1, 0, 0, 0, 0, 0])
# if delta_e < 0 or coin:
self.current_s = copy.deepcopy(self.next_s)
def get_status(self):
return self.current_s, self.cost_current_s
Visualization#
# Simulated Annealing part for evaluation script
iterations = 500
k, lam = get_SA_parameters(drivers, riders, eval_obj, iterations, adaptive=False)
start = time.time()
hist_solutions, hist_costs = runSA(
drivers, riders, graph, eval_obj, k, lam, iterations, adaptive=False)
end = time.time()
print("")
print("SA time = {} seconds".format(end - start))
100%|██████████| 500/500 [00:00<00:00, 792.95it/s]
SA time = 0.6326920986175537 seconds
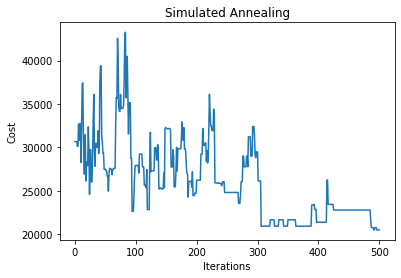
plt.plot(hist_costs)
plt.xlabel("Iterations")
plt.ylabel("Cost")
plt.title("Simulated Annealing")
print(f"Final cost:{hist_costs[-1]}")
plt.show()
Final cost:20512.625309653413
Solution 2: Genetic Algorithm#
Solver Class#
class GeneticSolver():
def __init__(self, drivers, riders, graph, evaluation, pop_size, crossover_rate=0.9, mutation_rate=0.1) -> None:
self.pop_size = pop_size
self.crossover_rate = crossover_rate
self.mutation_rate = mutation_rate
self.drivers = list(drivers)
self.riders = list(riders)
self.graph = graph
self.evaluation_obj = evaluation
self.debug = False
self.population = self.initialize_population()
self.best_score = float("inf")
def initialize_population(self):
population = list()
# generate solutions
for i in range(0, self.pop_size):
sol = self.generate_solution()
population.append(sol)
return population
def crossover(self):
max_num_children = self.pop_size//2
for i in range(0, max_num_children):
if random.uniform(0, 1) < self.crossover_rate:
p1, p2 = random.sample(self.population, 2)
# init child
num_drivers = len(self.drivers)
child1 = [list() for dr in range(0, num_drivers)]
# Take permutation from P1 and driver assignment structure from P2
# permutation of P1 - flatten
permutation_p1 = [item for sublist in p1 for item in sublist]
# Assign based on P2
assignments = 0
for driver_idx, driver_list in enumerate(p2):
child1[driver_idx] = permutation_p1[assignments:assignments + len(driver_list)]
assignments += len(driver_list)
# check
if self.debug:
flat_list = [item for sublist in child1 for item in sublist]
assert len(flat_list) == len(self.riders)
self.population.append(child1)
child2 = [list() for dr in range(0, num_drivers)]
# Take permutation from P2 and driver assignment structure from P1
# permutation of P2 - flatten
permutation_p2 = [item for sublist in p2 for item in sublist]
# Assign based on P2
assignments = 0
for driver_idx, driver_list in enumerate(p1):
child2[driver_idx] = permutation_p2[assignments:assignments + len(driver_list)]
assignments += len(driver_list)
# check
if self.debug:
flat_list = [item for sublist in child2 for item in sublist]
assert len(flat_list) == len(self.riders)
self.population.append(child2)
# inplace switch two driver assignments
def mutate_driver_assignment(self):
for p in self.population:
if random.uniform(0, 1) < self.mutation_rate:
selected_drivers = random.sample(range(0, len(self.drivers)), 2)
driver_a_idx = selected_drivers[0]
driver_b_idx = selected_drivers[1]
driver_a = p[driver_a_idx][:]
driver_b = p[driver_b_idx][:]
p[driver_a_idx] = driver_b
p[driver_b_idx] = driver_a
# inplace switch two riders
def mutate_rider_sequence(self):
for p in self.population:
if random.uniform(0, 1) < self.mutation_rate:
permutations = [item for sublist in p for item in sublist]
selected_riders = random.sample(range(0, len(self.riders)), 2)
rider_1_idx = selected_riders[0]
rider_2_idx = selected_riders[1]
rider_id_1 = permutations[rider_1_idx]
rider_id_2 = permutations[rider_2_idx]
mutated_permutations = permutations
mutated_permutations[rider_1_idx] = rider_id_2
mutated_permutations[rider_2_idx] = rider_id_1
assignments = 0
for driver_idx, driver_list in enumerate(p):
p[driver_idx] = mutated_permutations[assignments:assignments + len(driver_list)]
assignments += len(driver_list)
def fitness_func(self):
best_score = float("inf")
cost_per_solution = []
for sol in self.population:
sol_obj = self.index_to_objects(sol)
self.evaluation_obj.set_solution(sol_obj)
cost = self.evaluation_obj.evaluate_cost_func()
cost_per_solution.append(cost)
if best_score > cost:
best_score = cost
# update best score
if self.best_score > best_score:
self.best_score = best_score
# sorted population based on cost per solution
self.population = [sorted_solution for _, sorted_solution in sorted(zip(cost_per_solution, self.population))]
# update population to be top 50% that minimize objective - Elitism
def select_parent(self):
# survival of the fittest
num_parents = self.pop_size//2
self.population = self.population[0:num_parents]
def index_to_objects(self, idx_sol):
sol_obj = list()
for driver_assignment in idx_sol:
driver_assignment_obj = []
for rider_idx in driver_assignment:
driver_assignment_obj.append(self.riders[rider_idx])
sol_obj.append(driver_assignment_obj)
return sol_obj
# returns a list of lists of indices representing assignments for each driver
def generate_solution(self):
num_riders = len(self.riders)
num_drivers = len(self.drivers)
# create list of empty lists
sol = [list() for dr in range(0, num_drivers)]
# generate random permutation of riders
riders_permutation = list(range(num_riders))
random.shuffle(riders_permutation)
# Getting N (drivers) random numbers whose sum is M (riders)
#https://stackoverflow.com/questions/2640053/getting-n-random-numbers-whose-sum-is-m/2640079#2640079
# Generate N-1 random numbers between 0 and 1
x = list(np.random.uniform(low = 0.0, high = 1.0, size = num_drivers-1))
# Add the numbers 0 and 1 themselves to the list and then sort them
x.extend([0, 1])
x.sort()
# Take the differences of adjacent numbers
diff = [x[i]-x[i-1] for i in range(1, len(x))]
driver_assigment = [int(item * num_riders) for item in diff]
sum_assignment = sum(driver_assigment)
#
num_unassigned = num_riders - sum_assignment
for i in range(0, num_unassigned):
driver_idx = random.randint(0, num_drivers-1)
driver_assigment[driver_idx]+=1
assert sum(driver_assigment) == num_riders
assert len(driver_assigment) == num_drivers
for driver_idx, s in enumerate(sol):
if driver_idx == 0:
s.extend(riders_permutation[0:driver_assigment[0]])
else:
assignments_so_far = sum(driver_assigment[0:driver_idx])
s.extend(riders_permutation[assignments_so_far:assignments_so_far + driver_assigment[driver_idx]])
if self.debug:
flat_list = [item for sublist in sol for item in sublist]
flat_list = list(set(flat_list))
assert len(flat_list) == num_riders
return sol
def run_GA(evaluation_object, drivers, riders, graph, initial_pop_size, iterations, crossover_rate=0.9, mutation_rate=0.5, adaptive=False):
scores = []
gs_solver = GeneticSolver(drivers, riders, graph, evaluation_object,
pop_size=initial_pop_size,
crossover_rate=crossover_rate, mutation_rate=mutation_rate)
initial_crossover_rate = gs_solver.crossover_rate
initial_mutation_rate = gs_solver.mutation_rate
final_crossover_rate = 0.6
final_mutation_rate = 0.2
if adaptive:
assert final_crossover_rate <= crossover_rate
assert final_mutation_rate <= mutation_rate
for i in tqdm(range(iterations)):
gs_solver.fitness_func()
gs_solver.select_parent()
gs_solver.crossover()
gs_solver.mutate_rider_sequence()
gs_solver.mutate_driver_assignment()
scores.append(gs_solver.best_score)
if adaptive:
gs_solver.crossover_rate -= (initial_crossover_rate - final_crossover_rate)/iterations
gs_solver.mutation_rate -= (initial_mutation_rate - final_mutation_rate)/iterations
gs_solver = None
return scores
start = time.time()
hist_costs = run_GA(eval_obj, drivers, riders, graph, initial_pop_size=300, iterations=500, crossover_rate=0.9, mutation_rate=0.4)
end = time.time()
print("")
print("GA time = {} seconds".format(end - start))
100%|██████████| 500/500 [00:35<00:00, 14.04it/s]
GA time = 35.630380392074585 seconds
Visualize#
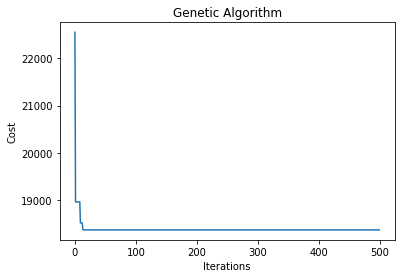
plt.plot(hist_costs)
plt.xlabel("Iterations")
plt.ylabel("Cost")
plt.title("Genetic Algorithm")
print(f"Final cost:{hist_costs[-1]}")
plt.show()
Final cost:18363.09688504041
Solution 3: Grey Wolf Algorithm#
You can read more about the Grey Wolf Optimizer here.
Wolf Class#
class Wolf():
def __init__(self, solution, eval_obj) -> None:
self._solution = solution
self._eval_obj = eval_obj
self._cost = None
self.update_cost()
@property
def solution(self):
return self._solution
@solution.setter
def solution(self, new_solution):
self._solution = new_solution
@property
def cost(self):
return self._cost
@cost.setter
def cost(self, new_cost):
self._cost = new_cost
def update_cost(self):
self._eval_obj.set_solution(self._solution)
self.cost = int(self._eval_obj.evaluate_cost_func())
def __eq__(self, other):
return self.cost == other.cost
def __lt__(self, other):
return self.cost < other.cost
def __repr__(self) -> str:
return f'This wolf\'s cost is {self._cost}'
Solver Class:#
class GWSolver():
def __init__(self, drivers, riders, graph, eval_obj, pack_size, max_hunt_range, iterations) -> None:
# validations
if pack_size <= 3:
raise ValueError('Pack size must be greater than 3')
if max_hunt_range < 1:
raise ValueError('Maximum hunting range must be >= 1')
# problem setup
self.drivers = drivers
self.riders = riders
self.graph = graph
self.eval_obj = eval_obj
self.iterations = iterations
self.iteration = 0
# grey wolf data
self.pack = []
self.leads = []
# pack_size determines the number of wolves in the pack
self.pack_size = pack_size
# max_hunt_range determines how many moves a wolf makes at an iteration
# begins high and reduces to very few moves at the end
self.max_hunt_range = max_hunt_range
self.current_hunt_range = max_hunt_range
# attack_rate determines how many wolves attack at a given iteration
# begins low and rises to all wolves attacking at the end
self.attack_rate = 3 # three leading wolves
# utilities
self.ns_generator = NeighborSolutions()
def generate_wolves_pack(self):
for i in range(self.pack_size):
rand_sol = copy.deepcopy(RandomSolution(
self.drivers, self.riders).get_random_sol())
a_wolf = Wolf(rand_sol, self.eval_obj)
self.pack.append(a_wolf)
def identify_lead_wolves(self):
self.pack.sort()
self.leads = self.pack[:3]
def update_hunting_range(self):
progress = self.iteration/self.iterations
num_moves = int((1-(progress))
* self.max_hunt_range)
self.current_hunt_range = num_moves
self.iteration += 1
def update_attack_rate(self):
progress = self.iteration/self.iterations
# three leading wolves
self.attack_rate = 3 + int(progress * (self.pack_size - 3))
def pack_hunts(self):
for i in range(self.attack_rate, self.pack_size):
# current wolf's solution
new_solution = copy.deepcopy(random.choice(self.leads).solution)
move = 0
while move <= self.current_hunt_range:
self.ns_generator.set_solution(new_solution)
new_solution = copy.deepcopy(random.choice(
self.ns_generator.get_neigbors()))
move += 1
self.pack[i] = Wolf(new_solution, self.eval_obj)
def get_status(self):
avg_cost = 0
for a_wolf in self.pack:
avg_cost += a_wolf.cost
avg_cost = avg_cost / self.pack_size
return avg_cost
def runGW(drivers, riders, graph, eval_obj, pack_size, max_hunt_range, iterations):
hist_costs = []
gw_solver = GWSolver(drivers, riders, graph, eval_obj,
pack_size, max_hunt_range, iterations)
gw_solver.generate_wolves_pack()
cost_i = gw_solver.get_status()
hist_costs.append(cost_i)
for i in tqdm(range(iterations)):
gw_solver.identify_lead_wolves()
gw_solver.update_hunting_range()
gw_solver.update_attack_rate()
gw_solver.pack_hunts()
cost_i = gw_solver.get_status()
hist_costs.append(cost_i)
return hist_costs
# Grey Wolf parameters
iterations = 500
pack_size = 10
max_hunt_range = 8
# Running GW
start = time.time()
hist_costs = runGW(drivers, riders, graph, eval_obj, pack_size, max_hunt_range, iterations)
end = time.time()
print(f'grey wolf time = {int(end - start)}')
print(f'grey wolf min cost {min(hist_costs)}')
100%|██████████| 500/500 [00:05<00:00, 91.77it/s]
grey wolf time = 5
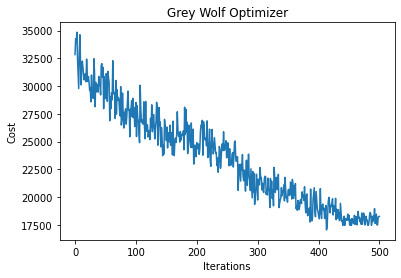
grey wolf min cost 17034.0
Visualize#
plt.plot(hist_costs)
plt.xlabel("Iterations")
plt.ylabel("Cost")
plt.title("Grey Wolf Optimizer")
print(f"Final cost:{hist_costs[-1]}")
plt.show()
Final cost:18249.4